4.3. Optimization
While the gradient descent algorithm has been used in the sample codes for optimizing gradients, more efficient options exist, as shown in Appendix 2.3.2.
This section introduces a powerful algorithm called Adam and showcases its capabilities.
Theoretical background of Adam:
- ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION (23.Jul.2015)
4.3.1. Implementation
Complete Python code is available at: Optimizer.py
4.3.1.1. Adam Class
Below is the Adam class:
#
# ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
# https://arxiv.org/pdf/1412.6980v8.pdf
#
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr # Learning rate
self.beta1 = beta1 # m's attenuation rate
self.beta2 = beta2 # v's attenuation rate
self.iter = 0
self.m = None # Momentum
self.v = None # Adaptive learning rate
def update(self, params, grads):
if self.m is None:
self.m = []
self.v = []
for param in params:
self.m.append(np.zeros_like(param))
self.v.append(np.zeros_like(param))
self.iter += 1
lr_t = (self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter))
for i in range(len(params)):
self.m[i] = (self.beta1 * self.m[i] + (1 - self.beta1) * grads[i])
self.v[i] = self.beta2 * self.v[i] + (1 - self.beta2) * (grads[i] ** 2)
params[i] -= lr_t * self.m[i] / (np.sqrt(self.v[i]) + 1e-7)4.3.1.2. update_weights() function
The update_weights() function serves as a wrapper for weight updates, capable of utilizing either Adam’s update function or gradient descent. It adaptively selects the optimization method based on the presence of the optimizer parameter:
- If the optimizer parameter is specified, the function calls Adam’s update function to adjust the weights.
- If the optimizer parameter is absent (i.e., $\text{optimizer} == \text{None}$), the function defaults to the gradient descent algorithm for weight updates.
def update_weights(layers, lr=0.01, optimizer=None, max_norm=None):
grads = []
params = []
for layer in layers:
grads.extend(layer.get_grads())
params.extend(layer.get_params())
# Clip gradient
if max_norm is not None:
grads = clip_gradient_norm(grads, max_norm)
# Weights and Bias Update
if optimizer == None:
# gradient descent
for i in range(len(grads)):
params[i] -= lr * grads[i]
else:
# ADAM
optimizer.update(params, grads)4.3.2. Demonstration
To provide a practical demonstration of Adam’s effectiveness compared to gradient descent, I developed a Python code named XOR-gate-adam.py. This code trains an XOR gate using both algorithms, allowing for direct performance comparison.
Here is a snippet of the Python code that is relevant to Adam.
dense = Layers.Dense(input_nodes, hidden_nodes, sigmoid, deriv_sigmoid)
dense_1 = Layers.Dense(hidden_nodes, output_nodes, sigmoid, deriv_sigmoid)
# ========================================
# Training
# ========================================
def train_adam(x, Y, optimizer):
# Forward Propagation
y = dense.forward_prop(x)
y = dense_1.forward_prop(y)
# Back Propagation
loss = np.sum((y - Y) ** 2 / 2)
dL = (y - Y)
dx = dense_1.back_prop(dL)
_ = dense.back_prop(dx)
# Weights and Bias Update
update_weights([dense, dense_1], optimizer=optimizer)
return loss
lr = 0.1
beta1 = 0.9
beta2 = 0.999
optimizer = Optimizer.Adam(lr=lr, beta1=beta1, beta2=beta2)
history_loss_adam = []
#
# Training loop
#
for epoch in range(1, n_epochs + 1):
loss = 0.0
for i in range(0, len(Y)):
loss += train_adam(X[i], Y[i], optimizer)Run the following command to execute the Python code and compare the performance of Adam and gradient descent algorithms on the XOR gate problem:
$ python XOR-gate-adam.py
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 3) 9
dense_1 (Dense) (None, 1) 4
=================================================================
Total params: 13
========= Gradient Descent =========
epoch: 1 / 10000 Loss = 0.670351
epoch: 1000 / 10000 Loss = 0.473633
epoch: 2000 / 10000 Loss = 0.374803
epoch: 3000 / 10000 Loss = 0.258562
epoch: 4000 / 10000 Loss = 0.091229
epoch: 5000 / 10000 Loss = 0.031913
epoch: 6000 / 10000 Loss = 0.016630
epoch: 7000 / 10000 Loss = 0.010774
epoch: 8000 / 10000 Loss = 0.007822
epoch: 9000 / 10000 Loss = 0.006079
epoch: 10000 / 10000 Loss = 0.004941
------------------------
x0 XOR x1 => result
========================
0 XOR 0 => 0.0556
0 XOR 1 => 0.9531
1 XOR 0 => 0.9532
1 XOR 1 => 0.0489
========================
========= ADAM =========
epoch: 1 / 10000 Loss = 0.579207
epoch: 1000 / 10000 Loss = 0.000240
epoch: 2000 / 10000 Loss = 0.000025
epoch: 3000 / 10000 Loss = 0.000003
epoch: 4000 / 10000 Loss = 0.000000
epoch: 5000 / 10000 Loss = 0.000000
epoch: 6000 / 10000 Loss = 0.000000
epoch: 7000 / 10000 Loss = 0.000000
epoch: 8000 / 10000 Loss = 0.000000
epoch: 9000 / 10000 Loss = 0.000000
epoch: 10000 / 10000 Loss = 0.000000
------------------------
x0 XOR x1 => result
========================
0 XOR 0 => 0.0000
0 XOR 1 => 1.0000
1 XOR 0 => 1.0000
1 XOR 1 => 0.0000
========================The results demonstrate that Adam converges significantly faster than gradient descent.
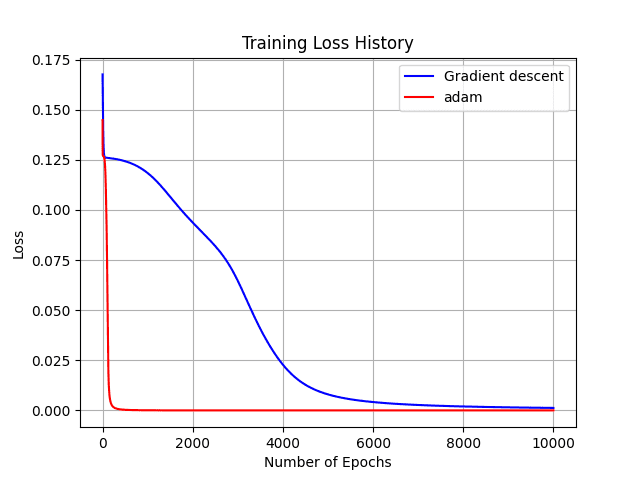
Although this is rare, convergence can be hindered by factors like initial values.