3.2. Cost Estimation in Single-Table Query
PostgreSQL’s query optimization is based on cost. Costs are dimensionless values, and they are not absolute performance indicators, but rather indicators to compare the relative performance of operations.
Costs are estimated by the functions defined in costsize.c. All operations executed by the executor have corresponding cost functions. For example, the costs of sequential scans and index scans are estimated by cost_seqscan() and cost_index(), respectively.
In PostgreSQL, there are three kinds of costs: start-up, run and total. The total cost is the sum of the start-up and run costs, so only the start-up and run costs are independently estimated.
- The start-up cost is the cost expended before the first tuple is fetched. For example, the start-up cost of the index scan node is the cost of reading index pages to access the first tuple in the target table.
- The run cost is the cost of fetching all tuples.
- The total cost is the sum of the costs of both start-up and run costs.
The EXPLAIN command shows both of start-up and total costs in each operation. The simplest example is shown below:
|
|
In Line 4, the command shows information about the sequential scan. In the cost section, there are two values; 0.00 and 145.00. In this case, the start-up and total costs are 0.00 and 145.00, respectively.
In this section, we will explore how to estimate the sequential scan, index scan, and sort operation in detail.
In the following explanations, we will use a specific table and an index that are shown below:
testdb=# CREATE TABLE tbl (id int PRIMARY KEY, data int);
testdb=# CREATE INDEX tbl_data_idx ON tbl (data);
testdb=# INSERT INTO tbl SELECT generate_series(1,10000),generate_series(1,10000);
testdb=# ANALYZE;
testdb=# \d tbl
Table "public.tbl"
Column | Type | Modifiers
--------+---------+-----------
id | integer | not null
data | integer |
Indexes:
"tbl_pkey" PRIMARY KEY, btree (id)
"tbl_data_idx" btree (data)3.2.1. Sequential Scan
The cost of the sequential scan is estimated by the cost_seqscan() function. In this subsection, we will explore how to estimate the sequential scan cost of the following query:
testdb=# SELECT * FROM tbl WHERE id <= 8000;In the sequential scan, the start-up cost is equal to 0, and the run cost is defined by the following equation:
$$ \begin{align} \text{'run cost'} &= \text{'cpu run cost'} + \text{'disk run cost'} \\ &= (\text{cpu_tuple_cost} + \text{cpu_operator_cost}) \times N_{tuple} + \text{seq_page_cost} \times N_{page} \end{align} $$where seq_page_cost, cpu_tuple_cost and cpu_operator_cost are set in the postgresql.conf file, and the default values are 1.0, 0.01, and 0.0025, respectively. $ N_{tuple} $ and $ N_{page} $ are the numbers of all tuples and all pages of this table, respectively. These numbers can be shown using the following query:
testdb=# SELECT relpages, reltuples FROM pg_class WHERE relname = 'tbl';
relpages | reltuples
----------+-----------
45 | 10000
(1 row)Therefore,
$$ \begin{align} \text{'run cost'} &= (0.01 + 0.0025) \times 10000 + 1.0 \times 45 = 170.0 \end{align} $$Finally,
$$ \begin{align} \text{'total cost'} = 0.0 + 170.0 = 170 \end{align} $$For confirmation, the result of the EXPLAIN command of the above query is shown below:
|
|
In Line 4, we can see that the start-up and total costs are 0.00 and 170.00, respectively. It is also estimated that 8000 rows (tuples) will be selected by scanning all rows.
In line 5, a filter ‘$\text{Filter}:(\text{id} \lt= 8000)$’ of the sequential scan is shown. More precisely, it is called a table level filter predicate.
Note that this type of filter is used when reading all the tuples in the table, and it does not narrow the scanned range of table pages.
As understood from the run-cost estimation, PostgreSQL assumes that all pages will be read from storage. In other words, PostgreSQL does not consider whether the scanned page is in the shared buffers or not.
3.2.2. Index Scan
Although PostgreSQL supports some index methods, such as BTree, GiST, GIN and BRIN, the cost of the index scan is estimated using the common cost function cost_index().
In this subsection, we explore how to estimate the index scan cost of the following query:
testdb=# SELECT id, data FROM tbl WHERE data <= 240;Before estimating the cost, the numbers of the index pages and index tuples, $ N_{index,page} $ and $ N_{index,tuple} $, are shown below:
testdb=# SELECT relpages, reltuples FROM pg_class WHERE relname = 'tbl_data_idx';
relpages | reltuples
----------+-----------
30 | 10000
(1 row)3.2.2.1. Start-Up Cost
The start-up cost of the index scan is the cost of reading the index pages to access the first tuple in the target table. It is defined by the following equation:
$$ \begin{align} \text{'start-up cost'} = \{\mathrm{ceil}(\log_2 (N_{index,tuple})) + (H_{index} + 1) \times 50\} \times \text{cpu_operator_cost} \end{align} $$where $ H_{index} $ is the height of the index tree.
In this case, according to (3), $ N_{index,tuple} $ is 10000, $ H_{index} $ is 1; $ \text{cpu_operator_cost} $ is $0.0025$ (by default). Therefore,
$$ \begin{align} \text{'start-up cost'} = \{\mathrm{ceil}(\log_2(10000)) + (1 + 1) \times 50\} \times 0.0025 = 0.285 \tag{5} \end{align} $$3.2.2.2. Run Cost
The run cost of the index scan is the sum of the CPU costs and the I/O (input/output) costs of both the table and the index:
$$ \begin{align} \text{'run cost'} &= (\text{'index cpu cost'} + \text{'table cpu cost'}) + (\text{'index IO cost'} + \text{'table IO cost'}). \end{align} $$If the Index-Only Scans, which is described in Section 7.2, can be applied, $ \text{’table cpu cost’} $ and $ \text{’table IO cost’} $ are not estimated.
The first three costs (i.e., index CPU cost, table CPU cost, and index I/O cost) are shown below:
$$ \begin{align} \text{'index cpu cost'} &= \text{Selectivity} \times N_{index,tuple} \times (\text{cpu_index_tuple_cost} + \text{qual_op_cost}) \\ \text{'table cpu cost'} &= \text{Selectivity} \times N_{tuple} \times \text{cpu_tuple_cost} \\ \text{'index IO cost'} &= \mathrm{ceil}(\text{Selectivity} \times N_{index,page}) \times \text{random_page_cost} \end{align} $$where:
- cpu_index_tuple_cost and random_page_cost are set in the postgresql.conf file. The defaults are 0.005 and 4.0, respectively.
- $ \text{qual_op_cost} $ is, roughly speaking, the cost of evaluating the index predicate. The default is 0.0025.
- $ \text{Selectivity} $ is the proportion of the search range of the index that satisfies the WHERE clause, it is a floating-point number from 0 to 1.
$ (\text{Selectivity} \times N_{tuple}) $ means the number of the table tuples to be read;
$ (\text{Selectivity} \times N_{index,page}) $ means the number of the index pages to be read.
Selectivity is described in detail in below.
The selectivity of query predicates is estimated using either the histogram_bounds or the MCV (Most Common Value), both of which are stored in the statistics information in the pg_stats.
Here, the calculation of the selectivity is briefly described using specific examples.
More details are provided in the official document.
The MCV of each column of a table is stored in the pg_stats view as a pair of columns named ‘most_common_vals’ and ‘most_common_freqs’:
- ‘most_common_vals’ is a list of the MCVs in the column.
- ‘most_common_freqs’ is a list of the frequencies of the MCVs.
Here is a simple example:
The table “countries” has two columns:
- a column ‘country’: This column stores the country name.
- a column ‘continent’: This column stores the continent name to which the country belongs.
testdb=# \d countries
Table "public.countries"
Column | Type | Modifiers
-----------+------+-----------
country | text |
continent | text |
Indexes:
"continent_idx" btree (continent)
testdb=# SELECT continent, count(*) AS "number of countries",
testdb-# (count(*)/(SELECT count(*) FROM countries)::real) AS "number of countries / all countries"
testdb-# FROM countries GROUP BY continent ORDER BY "number of countries" DESC;
continent | number of countries | number of countries / all countries
---------------+---------------------+-------------------------------------
Africa | 53 | 0.274611398963731
Europe | 47 | 0.243523316062176
Asia | 44 | 0.227979274611399
North America | 23 | 0.119170984455959
Oceania | 14 | 0.0725388601036269
South America | 12 | 0.0621761658031088
(6 rows)Consider the following query, which has a WHERE clause, ‘continent = ‘Asia’’:
testdb=# SELECT * FROM countries WHERE continent = 'Asia';In this case, the planner estimates the index scan cost using the MCV of the ‘continent’ column. The ‘most_common_vals’ and ‘most_common_freqs’ of this column are shown below:
testdb=# \x
Expanded display is on.
testdb=# SELECT most_common_vals, most_common_freqs FROM pg_stats
testdb-# WHERE tablename = 'countries' AND attname='continent';
-[ RECORD 1 ]-----+-------------------------------------------------------------
most_common_vals | {Africa,Europe,Asia,"North America",Oceania,"South America"}
most_common_freqs | {0.274611,0.243523,0.227979,0.119171,0.0725389,0.0621762}The value of most_common_freqs corresponding to ‘Asia’ of the most_common_vals is 0.227979. Therefore, 0.227979 is used as the selectivity in this estimation.
If the MCV cannot be used, e.g., the target column type is integer or double precision, then the value of the histogram_bounds of the target column is used to estimate the cost.
- histogram_bounds is a list of values that divide the column’s values into groups of approximately equal population.
A specific example is shown. This is the value of the histogram_bounds of the column ‘data’ in the table ’tbl’:
testdb=# SELECT histogram_bounds FROM pg_stats WHERE tablename = 'tbl' AND attname = 'data';
histogram_bounds
---------------------------------------------------------------------------------------------------
{1,100,200,300,400,500,600,700,800,900,1000,1100,1200,1300,1400,1500,1600,1700,1800,1900,2000,2100,
2200,2300,2400,2500,2600,2700,2800,2900,3000,3100,3200,3300,3400,3500,3600,3700,3800,3900,4000,4100,
4200,4300,4400,4500,4600,4700,4800,4900,5000,5100,5200,5300,5400,5500,5600,5700,5800,5900,6000,6100,
6200,6300,6400,6500,6600,6700,6800,6900,7000,7100,7200,7300,7400,7500,7600,7700,7800,7900,8000,8100,
8200,8300,8400,8500,8600,8700,8800,8900,9000,9100,9200,9300,9400,9500,9600,9700,9800,9900,10000}
(1 row)By default, the histogram_bounds is divided into 100 buckets. Figure 3.7 illustrates the buckets and the corresponding histogram_bounds in this example. Buckets are numbered starting from 0, and every bucket stores (approximately) the same number of tuples. The values of histogram_bounds are the bounds of the corresponding buckets. For example, the 0th value of the histogram bounds is 1, which means that it is the minimum value of the tuples stored in bucket 0. The 1st value is 100 and this is the minimum value of the tuples stored in bucket 1, and so on.
Figure 3.7. Buckets and histogram_bounds.
Next, the calculation of the selectivity will be shown using the example in this subsection. The query has a WHERE clause ‘$\text{data} \lt= 240$’ and the value 240 is in the second bucket. In this case, the selectivity can be derived by applying linear interpolation. Thus, the selectivity of the column ‘data’ in this query is calculated using the following equation:
$$ \begin{align} \text{Selectivity} &= \frac{2 + (240-\text{hb[2]})/(\text{hb[3]} - \text{hb[2]})}{100} \\ &= \frac{2 + (240-200) / (300-200)}{100} = \frac{2 + 40/100}{100} \\ &= 0.024 \tag{6} \end{align} $$Thus, according to (1),(3),(4) and (6),
$$ \begin{align} \text{'index cpu cost'} &= 0.024 \times 10000 \times (0.005 + 0.0025) = 1.8 \tag{7} \\ \text{'table cpu cost'} &= 0.024 \times 10000 \times 0.01 = 2.4 \tag{8} \\ \text{'index IO cost'} &= \mathrm{ceil}(0.024 \times 30) \times 4.0 = 4.0 \tag{9} \end{align} $$$ \text{’table IO cost’} $ is defined by the following equation:
$$ \begin{align} \text{'table IO cost'} = \text{max_IO_cost} + \text{indexCorrelation}^2 \times (\text{min_IO_cost} - \text{max_IO_cost}) \end{align} $$$ \text{max_IO_cost} $ is the worst case of the IO cost, that is, the cost of randomly scanning all table pages; this cost is defined by the following equation:
$$ \begin{align} \text{max_IO_cost} = N_{page} \times \text{random_page_cost} \end{align} $$In this case, according to (2), $ N_{page} = 45 $, and thus
$$ \begin{align} \text{max_IO_cost} = 45 \times 4.0 = 180.0 \tag{10} \end{align} $$$ \text{min_IO_cost} $ is the best case of the IO cost, that is, the cost of sequentially scanning the selected table pages; this cost is defined by the following equation:
$$ \begin{align} \text{min_IO_cost} = 1 \times \text{random_page_cost} + (\mathrm{ceil}(\text{Selectivity} \times N_{page}) - 1) \times \text{seq_page_cost} \end{align} $$In this case,
$$ \begin{align} \text{min_IO_cost} = 1 \times 4.0 + (\mathrm{ceil}(0.024 \times 45)) - 1) \times 1.0 = 5.0 \tag{11} \end{align} $$$ \text{indexCorrelation} $ is described in detail in below, and in this example,
$$ \begin{align} \text{indexCorrelation} = 1.0 \tag{12} \end{align} $$Thus, according to (10),(11) and (12),
$$ \begin{align} \text{'table IO cost'} = 180.0 + 1.0^2 \times (5.0 - 180.0) = 5.0 \tag{13} \end{align} $$Finally, according to (7),(8),(9) and (13),
$$ \begin{align} \text{'run cost'} = (1.8 + 2.4) + (4.0 + 5.0) = 13.2 \tag{14} \end{align} $$Index correlation is a statistical correlation between the physical row ordering and the logical ordering of the column values (cited from the official document). This ranges from -1 to +1. To understand the relation between the index scan and the index correlation, a specific example is shown below.
The table ’tbl_corr’ has five columns: two columns are text type and three columns are integer type. The three integer columns store numbers from 1 to 12. Physically, tbl_corr is composed of three pages, and each page has four tuples. Each integer type column has an index with a name such as index_col_asc and so on.
testdb=# \d tbl_corr
Table "public.tbl_corr"
Column | Type | Modifiers
----------+---------+-----------
col | text |
col_asc | integer |
col_desc | integer |
col_rand | integer |
data | text |
Indexes:
"tbl_corr_asc_idx" btree (col_asc)
"tbl_corr_desc_idx" btree (col_desc)
"tbl_corr_rand_idx" btree (col_rand)testdb=# SELECT col,col_asc,col_desc,col_rand
testdb-# FROM tbl_corr;
col | col_asc | col_desc | col_rand
----------+---------+----------+----------
Tuple_1 | 1 | 12 | 3
Tuple_2 | 2 | 11 | 8
Tuple_3 | 3 | 10 | 5
Tuple_4 | 4 | 9 | 9
Tuple_5 | 5 | 8 | 7
Tuple_6 | 6 | 7 | 2
Tuple_7 | 7 | 6 | 10
Tuple_8 | 8 | 5 | 11
Tuple_9 | 9 | 4 | 4
Tuple_10 | 10 | 3 | 1
Tuple_11 | 11 | 2 | 12
Tuple_12 | 12 | 1 | 6
(12 rows)The index correlations of these columns are shown below:
testdb=# SELECT tablename,attname, correlation FROM pg_stats WHERE tablename = 'tbl_corr';
tablename | attname | correlation
-----------+----------+-------------
tbl_corr | col_asc | 1
tbl_corr | col_desc | -1
tbl_corr | col_rand | 0.125874
(3 rows)When the following query is executed, PostgreSQL reads only the first page because all of the target tuples are stored in the first page. See Figure 3.8(a).
testdb=# SELECT * FROM tbl_corr WHERE col_asc BETWEEN 2 AND 4;On the other hand, when the following query is executed, PostgreSQL has to read all pages. See Figure 3.8(b).
testdb=# SELECT * FROM tbl_corr WHERE col_rand BETWEEN 2 AND 4;In this way, the index correlation is a statistical correlation that reflects the impact of random access caused by the discrepancy between the index ordering and the physical tuple ordering in the table when estimating the index scan cost.
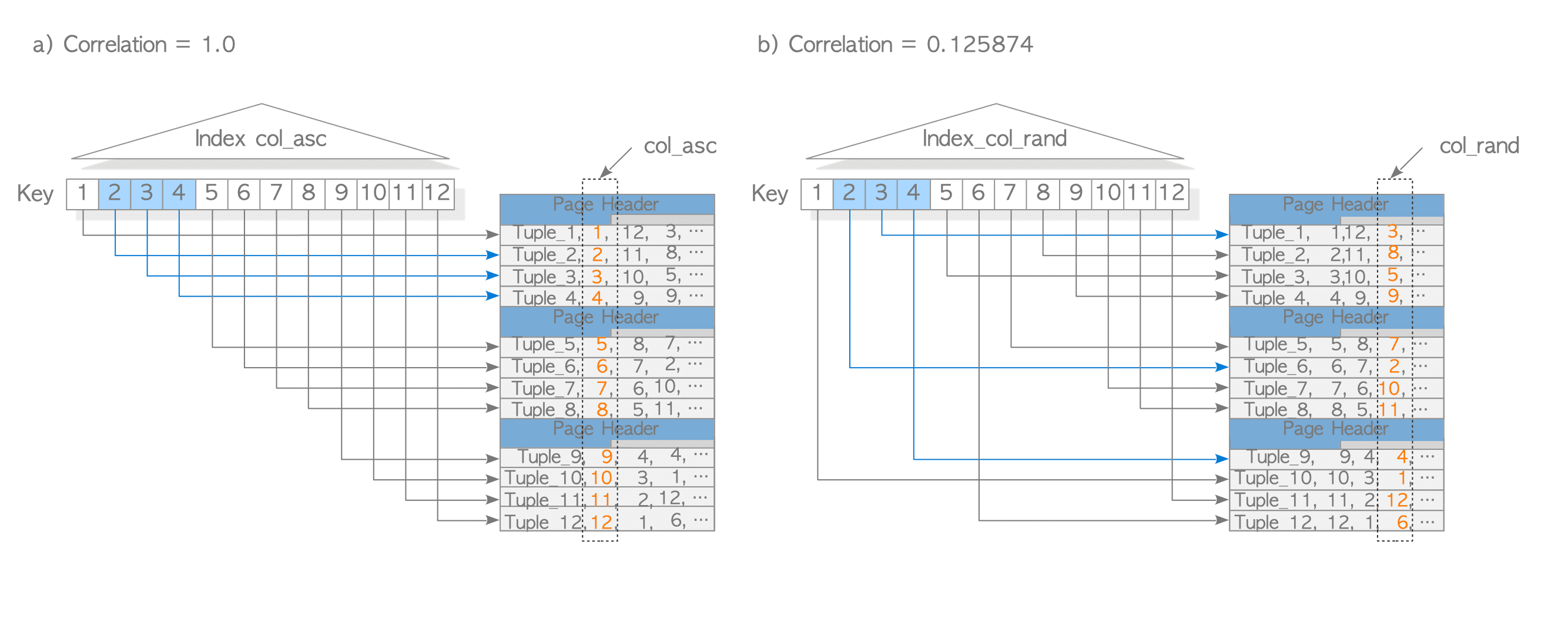
Figure 3.8. Index correlation.
3.2.2.3. Total Cost
According to (3) and (14),
$$ \begin{align} \text{'total cost'} = 0.285 + 13.2 = 13.485 \tag{15} \end{align} $$For confirmation, the result of the EXPLAIN command of the above SELECT query is shown below:
|
|
In Line 4, we can find that the start-up and total costs are 0.29 and 13.49, respectively, and it is estimated that 240 rows (tuples) will be scanned.
In Line 5, an index condition ‘$\text{Index} \text{Cond}:(\text{data} \lt= 240)$’ of the index scan is shown. More precisely, this condition is called an access predicate, and it expresses the start and stop conditions of the index scan.
According to this post, EXPLAIN command in PostgreSQL does not distinguish between the access predicate and index filter predicate. Therefore, when analyzing the output of EXPLAIN, it is important to consider both the index conditions and the estimated value of rows.
The default values of seq_page_cost and random_page_cost are 1.0 and 4.0, respectively.
This means that PostgreSQL assumes that the random scan is four times slower than the sequential scan. In other words, the default value of PostgreSQL is based on using HDDs.
On the other hand, in recent days, the default value of random_page_cost is too large because SSDs are mostly used. If the default value of random_page_cost is used despite using an SSD, the planner may select ineffective plans. Therefore, when using an SSD, it is better to change the value of random_page_cost to 1.0.
This blog reported the problem when using the default value of random_page_cost.
3.2.3. Sort
The sort path is used for sorting operations, such as ORDER BY, the preprocessing of merge join operations, and other functions. The cost of sorting is estimated using the cost_sort() function.
In the sorting operation, if all tuples to be sorted can be stored in work_mem, the quicksort algorithm is used. Otherwise, a temporary file is created and the file merge sort algorithm is used.
The start-up cost of the sort path is the cost of sorting the target tuples. Therefore, the cost is $ O(N_{sort} \times \log_2(N_{sort})) $, where $ N_{sort} $ is the number of the tuples to be sorted. The run cost of the sort path is the cost of reading the sorted tuples. Therefore the cost is $ O(N_{sort}) $.
In this subsection, we explore how to estimate the sorting cost of the following query. Assume that this query will be sorted in work_mem, without using temporary files.
testdb=# SELECT id, data FROM tbl WHERE data <= 240 ORDER BY id;In this case, the start-up cost is defined in the following equation:
$$ \begin{align} \text{'start-up cost'} = C + \text{comparison_cost} \times N_{sort} \times \log_2(N_{sort}) \end{align} $$where:
- $ C $ is the total cost of the last scan, that is, the total cost of the index scan; according to (15), it is 13.485.
- $ N_{sort} $ is the number of tuples to be sorted. In this case, it is 240.
- $ \text{comparison_cost} $ is defined in $ 2 \times \text{cpu_operator_cost} $.
Therefore, the $ \text{start-up cost} $ is calculated as follows:
$$ \begin{align} \text{'start-up cost'} = 13.485 + (2 \times 0.0025) \times 240.0 \times \log_2(240.0) = 22.973 \end{align} $$The $ \text{run cost} $ is the cost of reading sorted tuples in the memory. Therefore,
$$ \begin{align} \text{'run cost'} = \text{cpu_operator_cost} \times N_{sort} = 0.0025 \times 240 = 0.6 \end{align} $$Finally,
$$ \begin{align} \text{'total cost'} = 22.973 + 0.6 = 23.573 \end{align} $$For confirmation, the result of the EXPLAIN command of the above SELECT query is shown below:
|
|
In line 4, we can find that the start-up cost and total cost are 22.97 and 23.57, respectively.