3.4. Executor Performance
This section explains how the executor processes queries and how aggregate functions are handled.
3.4.1. How the Executor Performs
In single-table queries, the executor takes the plan nodes in an order from the end of the plan tree to the root and then invokes the functions that perform the processing of the corresponding nodes.
Each plan node has functions that are meant for executing the respective operation. These functions are located in the src/backend/executor/ directory.
For example, the functions for executing the sequential scan (SeqScan) are defined in nodeSeqscan.c; the functions for executing the index scan (IndexScanNode) are defined in nodeIndexscan.c; the functions for sorting SortNode are defined in nodeSort.c, and so on.
The best way to understand how the executor performs is to read the output of the EXPLAIN command. PostgreSQL’s EXPLAIN shows the plan tree almost as it is. It will be explained using Example 1 in Section 3.3.3.1.
|
|
Let’s explore how the executor performs. Read the result of the EXPLAIN command from the bottom line to the top line.
-
Line 6: The SeqScan node, defined in nodeSeqscan.c, sequentially scans the target table and sends tuples to the SortNode.
-
Line 4: The SortNode receives tuples one by one from the SeqScan node, stores them in the work_mem buffer, and sorts the tuples after the SeqScan is complete.
Figure 3.16 illustrates how the sort processing works.
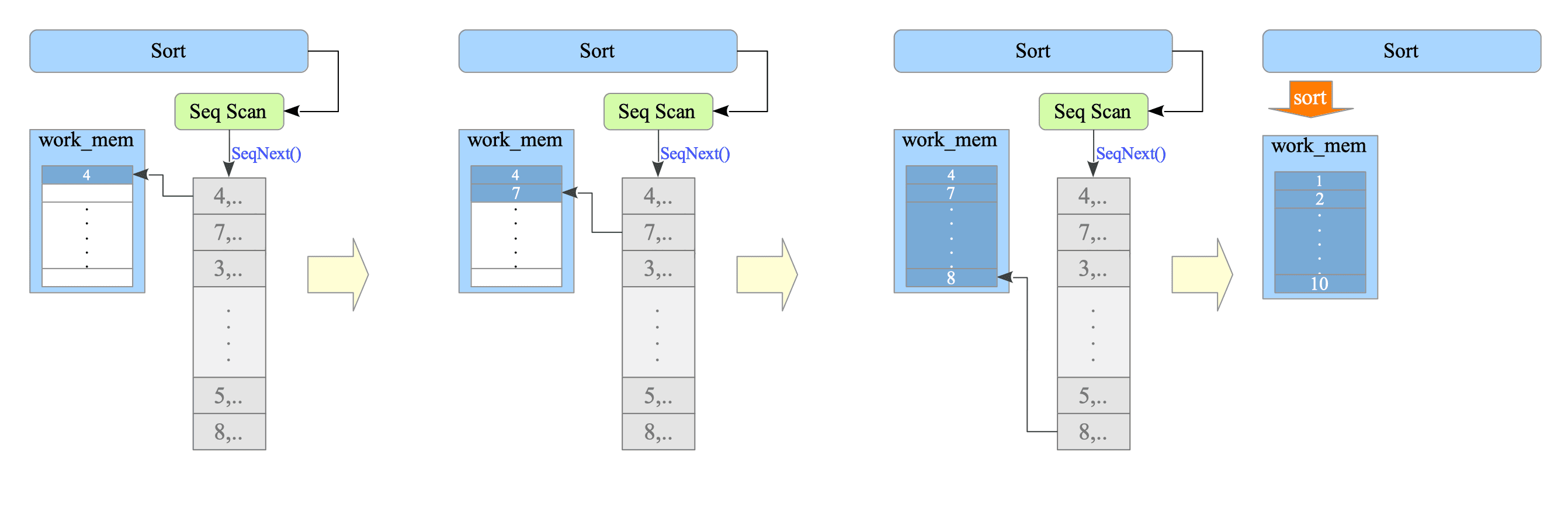
Figure 3.16. Sort Processing in the Executor.
From the Executor’s perspective, it starts a SortNode, runs a SeqScan within the SortNode to obtain tuples sequentially, and then sorts these tuples in memory (work_mem).
3.4.1.1. Scanning Functions
As mentioned in Section 1.3, data tuples are stored in 8KB physical blocks. To access a single data tuple, the Executor must traverse many layers, such as Buffer Manager (see Chapter 8) and Concurrency Control (see Chapter 5). Furthermore, the access method differs depending on whether the data block belongs to a table or an index.
The method of accessing a single data tuple by the Executor is highly abstracted, and the complexity of the intermediate layers is hidden.
For example, in the case of a sequential scan, by repeatedly calling the SeqNext() function, rows in a table can be accessed sequentially, taking transactions into account. For an index scan, an index scan can be performed by repeatedly calling the IndexNext() function.
3.4.1.2. Temporary Files
Although the executor uses the work_men and temp_buffers, which are allocated in the memory, for query processing, it uses temporary files if the processing cannot be performed within the memory alone.
Using the ANALYZE option, the EXPLAIN command actually executes the query and displays the true row counts, true run time, and the actual memory usage. A specific example is shown below:
|
|
In Line 6, the EXPLAIN command shows that the executor has used a temporary file whose size is 10000kB.
Temporary files are created in the base/pg_tmp subdirectory temporarily, and the naming method is shown follows:
{"pgsql_tmp"} + {PID of the postgres process which creates the file} . {sequencial number from 0}For example, the temporary file ‘pgsql_tmp8903.5’ is the 6th temporary file created by the postgres process with the pid of 8903.
$ ls -la /usr/local/pgsql/data/base/pgsql_tmp*
-rw------- 1 postgres postgres 10240000 12 4 14:18 pgsql_tmp8903.53.4.2. Aggregate Functions
In practice, calculating aggregate functions is also an important role of the database systems. We briefly explore how aggregate functions are handled, using sum, average and variance.
In the following, we use the following table d:
testdb=# CREATE TABLE d (x DOUBLE PRECISION);
CREATE TABLE
testdb=# INSERT INTO d SELECT GENERATE_SERIES(1, 10);
INSERT 0 10For example, when the sum function is issued, the following plan tree (Figure 3.17) is created.
testdb=# SELECT sum(x) FROM d;
sum
-----
55
(1 row)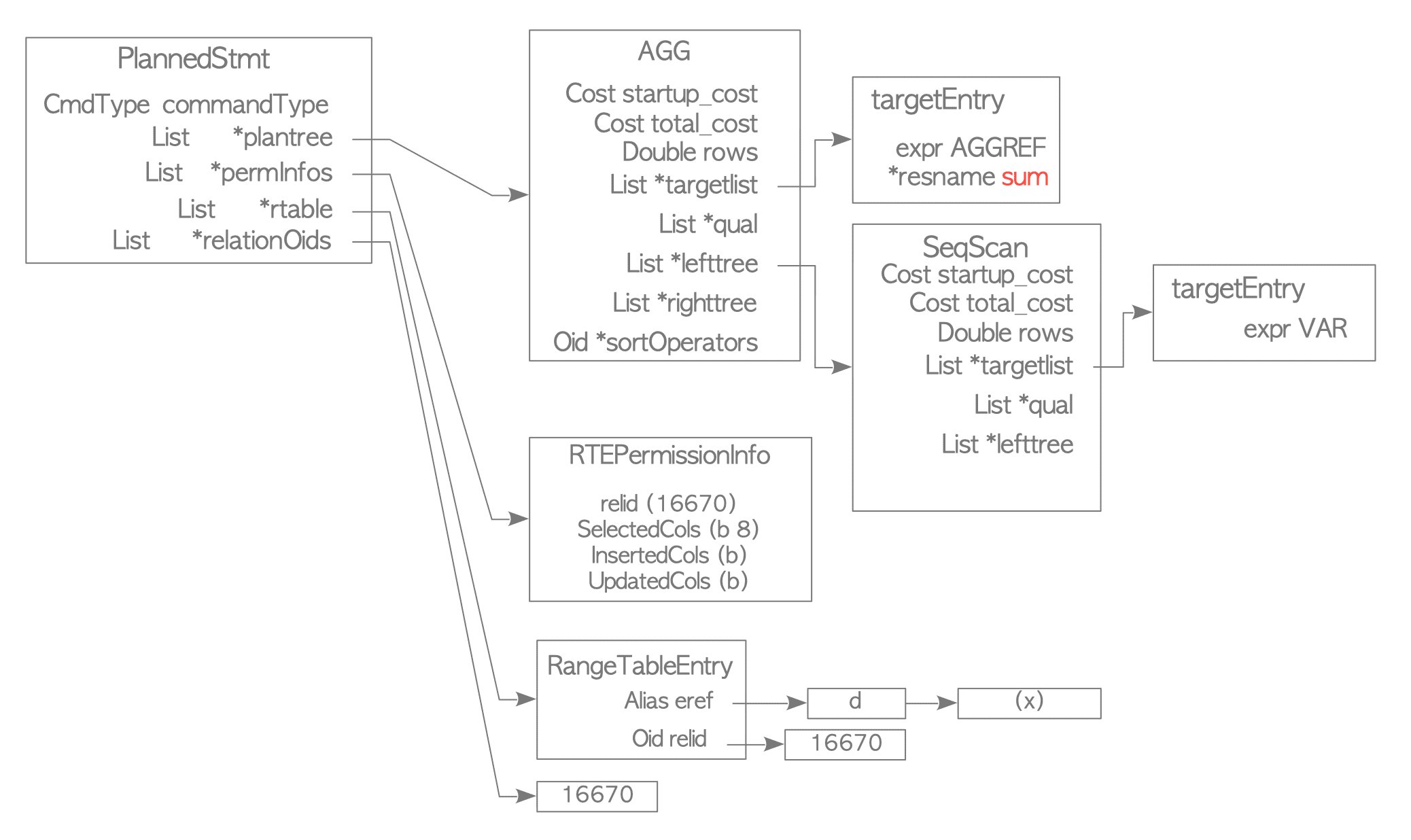
Figure 3.17. A Plan Tree for the Sum Function.
The result of the EXPLAIN command is shown below:
|
|
-
Line 5: The SeqScan node sequentially scans the target table and sends the value of the target column (datum) to the AggregateNode.
-
Line 4: The AggregateNode receives the datum from the SeqScan node and processes it according to the specified aggregate function (e.g., sum, average, variance, count, etc.).
Figure 3.18 orverviews how the aggregate function is processed.
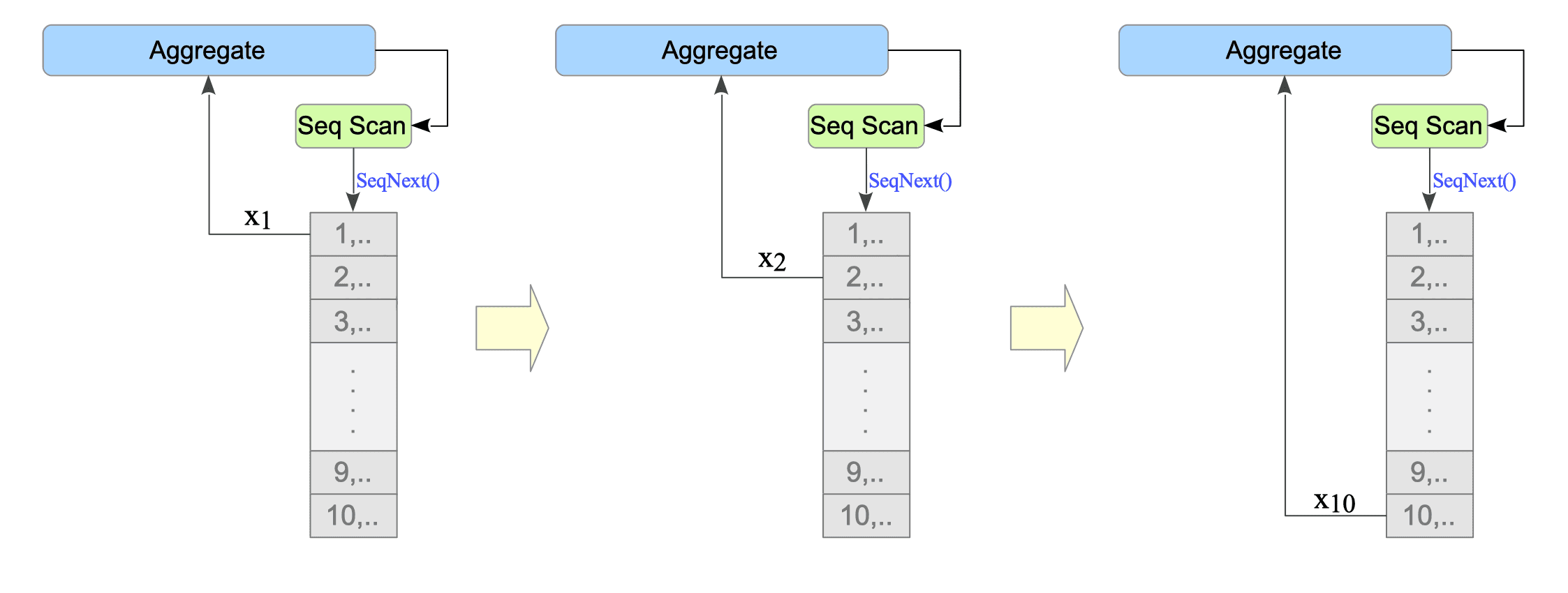
Figure 3.18. Aggregate Function Processing in the Executor.
In the following subsections, we will explore how aggregate functions are processed using concrete examples.
3.4.2.1. Sum and Average
The formulas for the sum $S_{n}$ and average $A_{n}$ are given by:
$$ \begin{align} S_{n} &= \sum_{i=1}^{n} x_{i} \tag{16} \\ A_{n} &= \frac{1}{n} \sum_{i=1}^{n} x_{i} = \frac{1}{n} S_{n} \tag{17} \end{align} $$where $x_{i}$ is the value of the target column at index $i$.
As is evident, the only difference between the sum and average is whether or not we divide by the number of elements, $n$.
Internally, an Aggregate node accumulates the scanned values sequentially.
When returning the result, it returns the sum for the sum operation, and the sum divided by $n$ for the average.
Following is the pseudocode.
d =[1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0]
N = 0
S = 0
# Seq Scan
for x in d:
# Aggregate: Sum
N += 1
S += x
print("Sum=", S)
print("Avg=", S/N)3.4.2.2. Variance
For simplicity, we define variance as follows:
$$ V_{n} = \sum_{i=1}^{n} (x_{i} - A_{n})^{2} \tag{18} $$From this definition, we can define:
- Sample Variance (var_samp): $\frac{1}{n-1} V_{n}$ (used when data represents a sample)
- Population Variance (var_pop): $\frac{1}{n} V_{n}$ (used when data represents the entire population)
testdb=# SELECT var_samp(x) FROM d;
var_samp
-------------------
9.166666666666666
(1 row)
testdb=# SELECT var_pop(x) FROM d;
var_pop
---------
8.25
(1 row)3.4.2.2.1. One-Pass Variance Calculation (Versions 11 or earlier)
A naive implementation of the variance formula $(18)$ requires two passes over the data: one to calculate the average and another to calculate the squared differences.
However, we can optimize this to a single-pass calculation using the following formula (For details, refer to the following ):
$$ \begin{align} V_{n} &= \sum_{i=1}^{n} x_{i}^{2} - \frac{1}{n} (S_{n})^{2} \tag{19} \\ \end{align} $$This allows us to calculate the variance in a single pass by iteratively calculating $x_{i}^{2}$ and $S_{i}$.
Following is the pseudocode.
d =[1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0]
N = 0
S = 0
X2 = 0
# SeqScan
for x in d:
# Aggregate: Variance
N += 1
S += x
X2 += x**2
V = X2 - S**2/N
print("V=", V)
print("Var_samp=", V/(N-1))
print("Var_pop=", V/N)3.4.2.2.2. Youngs and Cramer method (Versions 12 or later)
A paper titled “A Closer Look at Variance ImplementationsIn Modern Database Systems” pointed out the low accuracy of PostgreSQL’s variance function in 2016.
To address this issue, a patch was created in November 2018, and the Youngs and Cramer method was subsequently adopted in version 12. This method offers a more accurate way to calculate variance.
$$ \begin{cases} V_{1} &= 0 \\ V_{n} &= V_{n-1} + \frac{1}{n(n-1)} (nx_{n} - S_{n})^{2} \tag{20} \end{cases} $$Following is the pseudocode of Youngs and Cramer method:
d =[1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0]
N = 0
S = 0
V = 0
# SeqScan
for x in d:
# Aggregate: Variance
N += 1
S += x
if 1 < N:
V += (x * N - S)**2 / (N * (N-1))
print("V=", V)
print("Var_samp=", V/(N-1))
print("Var_pop=", V/N)The Youngs and Cramer method is an improvement on the Welfold method. To derive the Youngs and Cramer method, we first examine the Welfold method.
Welfold method:
The Welfold method for calculating variance is defined as follows:
$$ V_{n} = V_{n-1} + \frac{n-1}{n} (x_{n} - A_{n-1})^{2} $$This can be rewritten as a recurrence relation:
$$ \begin{align} V_{n} &= \sum_{i=1}^{n} (x_{i} - A_{n})^{2} = \sum_{i=1}^{n-1} (x_{i} - A_{n})^{2} + (x_{n} - A_{n})^{2} \\ &= \sum_{i=1}^{n-1} \left( (x_{i} - \frac{1}{n}((n-1)A_{n-1} + x_{n}) \right)^{2} + \left( (x_{n} - \frac{1}{n}((n-1)A_{n-1} + x_{n}) \right)^{2} \\ &= \sum_{i=1}^{n-1} \left( (x_{i} - A_{n-1}) - \frac{1}{n}(x_{n} - A_{n-1}) \right)^{2} + \left( \frac{1}{n} (nx_{n} - (n-1)A_{n-1} - x_{n} ) \right)^{2} \\ &= \sum_{i=1}^{n-1} \left( (x_{i} - A_{n-1})^{2} - \frac{2(x_{n} - A_{n-1})}{n}(x_{i} - A_{n-1}) + \frac{1}{n^{2}}(x_{n} - A_{n-1})^{2} \right) \\ & \quad + \left( \frac{(n - 1) x_{n} - (n-1) A_{n-1}}{n} \right)^{2} \\ &= \sum_{i=1}^{n-1} (x_{i} - A_{n-1})^{2} - \frac{2(x_{n} - A_{n-1})}{n} \sum_{i=1}^{n-1}(x_{i} - A_{n-1}) + \frac{1}{n^{2}} \sum_{i=1}^{n-1} (x_{n} - A_{n-1})^{2} \\ & \quad + \left( \frac{(n - 1) (x_{n} - A_{n-1})}{n} \right)^{2} \\ &= V_{n-1} - \frac{2(x_{n} - A_{n-1})}{n} \left( \sum_{i=1}^{n-1} x_{i} - (n-1)A_{n-1} \right) + \frac{1}{n^{2}} (n-1) \cdot (x_{n} - A_{n-1})^{2} \\ & \quad + \left( \frac{n-1}{n} \right)^{2} (x_{n} - A_{n-1})^{2} \\ &= V_{n-1} - \frac{2(x_{n} - A_{n-1})}{n} (S_{n-1} - S_{n-1}) + \left( \frac{n-1}{n^{2}} + \left( \frac{n-1}{n}\right)^{2} \right) (x_{n} - A_{n-1})^{2} \\ &= V_{n-1} - \frac{2(x_{n} - A_{n-1})}{n} \cdot 0 + \frac{(n-1) + (n-1)^{2}}{n^{2}} (x_{n} - A_{n-1})^{2} \\ &= V_{n-1} + \frac{(n-1)(1 + (n-1))}{n^{2}} (x_{n} - A_{n-1})^{2} \\ &= V_{n-1} + \frac{n-1}{n} (x_{n} - A_{n-1})^{2} \end{align} $$Youngs and Cramer method:
The Youngs and Cramer method is a modification of the Welfold method, where the average $A_{n-1}$ is replaced by the sum $S_{n-1}$ and further optimizations are made. The recurrence relation for the Youngs and Cramer method is:
$$ \begin{align} V_{n} &= V_{n-1} + \frac{n-1}{n} \left( x_{n} - \frac{S_{n-1}}{n-1} \right)^{2} = V_{n-1} + \frac{n-1}{n} \left( \frac{(n-1)x_{n} - S_{n-1}}{n-1} \right)^{2} \\ &= V_{n-1} + \frac{1}{n(n-1)} ((n-1)x_{n} - S_{n-1})^{2} = V_{n-1} + \frac{1}{n(n-1)} (nx_{n} - x_{n} - (S_{n}- x_{n} ))^{2} \\ &= V_{n-1} + \frac{1}{n(n-1)} (nx_{n} - S_{n})^{2} \end{align} $$