2.3. Gradient Descent Algorithms

From a mathematical perspective, deep learning solves optimization problems to determine the optimal model parameters for a given task. Therefore, a foundational understanding of optimization algorithms is crucial for those working in this field.

2.3.1. Gradient Descent Algorithm

Gradient descent (GD) is an iterative algorithm that utilizes the gradient of a function to find its minimum. Its simplicity makes it a fundamental building block for many optimization problems.

Formulation:

Given a differentiable function $L(x)$, where $x$ represents a vector of parameters, we can compute the value of $x_{min}$ that minimizes $L(x)$, denoted by $ x_{min} = \underset{x}{argmin} \ L(x)$, using the following iterative rule:

where:

• $\eta$ (eta): Learning rate, a positive hyperparameter $(0 \lt \eta)$ that controls the step size of the update.

• $\nabla$ (nabla): Gradient operator, e.g., $\nabla L(x_{1}, x_{2}, \ldots, x_{n}) = (\frac{\partial L}{\partial x_{1}},\frac{\partial L}{\partial x_{2}}, \ldots, \frac{\partial L}{\partial x_{n}})^{T}$

Example:

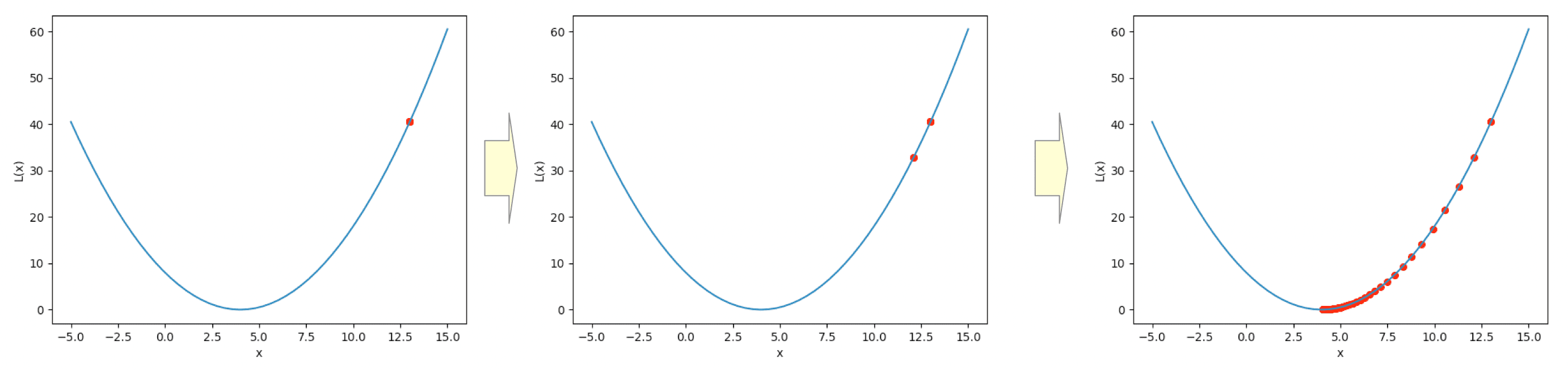
Let’s compute the minimum value (denoted by $x_{min}$) that minimizes the following function:

In this example, the gradient of the function $L(x)$ is:

Using these, we can compute the $x_{min}$ as follows:

def dL(x):
    # Calculates the gradient of the function L(x) at a given x.
    return (x - 4)

# learning rate
lr = 0.1

# Initialize x with a value further from the minimum for better visualization
x = 14

# Training loop
for epoch in range(100):
    # update x
    x = x - lr * dL(x)

Complete Python code is available at: gd.py

Run the following command to compute the $x_{min}$ and $L(x_{min})$:

$ python gd.py
x_min = 4.000	=> L(4.000) = 0.000

This Python code additionally generates an animation visualizing the gradient descent algorithm.

2.3.2. Stochastic Gradient Descent Algorithms

Despite its simplicity, vanilla Gradient Descent has three main disadvantages:

1. Slowness: Processing all training data at once makes it time-consuming.
2. Learning Rate Tuning: Choosing the right learning rate requires careful adjustment.
3. Local Minima Traps: It can get stuck at points that are not the absolute minimum.

To deal with these disadvantages, many stochastic gradient descent algorithms have been developed:

• Adam
• Adagrad
• Adadelta
• Adamax
• Nadam
• RMSprop

These algorithms are readily available in deep learning frameworks like TensorFlow and PyTorch.