17.1. Multi-Head Attention
As mentioned in Section 15.2.1.1, while multi-head attention is the core of the Transformer, its computational complexity limits both the maximum sequence length it can handle and its overall performance.
To address these bottlenecks, researchers have proposed numerous variants, exceeding a hundred in number.
This explanation will focus on some key variants and methods that have significantly impacted the development of mainstream large language models (LLMs).
- Efficient Transformers: A Survey (v1: 14.Mar.2022, v3: 14.Mar.2022)
- A Practical Survey on Faster and Lighter Transformers (v1: 26.Mar.2021, v2: 27.Mar.2023)
- Efficient Attention Mechanisms for Large Language Models: A Survey (v1: 25.Jul.2025, v2: 7.Aug.2025)
This explanation is restricted to publicly available information. While advanced commercial systems like GPT-3.5 (32k tokens) and Claude-2 (100k tokens) can process impressively long sequences, their internal workings remain undisclosed.
Even though this field is evolving rapidly, making it impossible to catch up with all developments, I will list some important developments that have emerged since this article was written.
- Infini-Attention Leave No Context Behind: Efficient Infinite Context Transformers with Infini-attention (v1: 10.Apr.2024, v2: 9.Aug.2024)
- Selective Attention Selective Attention Improves Transformer (v1: 3.Oct.2024)
- Differential Attention Differential Transformer (v1: 7.Oct.2024)
- Duo Attention DuoAttention: Efficient Long-Context LLM Inference with Retrieval and Streaming Heads (v1: 14.Oct.2024)
- Star Attention Star Attention: Efficient LLM Inference over Long Sequences (v1: 26.Nov.2024)
- LASER LASER: Attention with Exponential Transformation (v1: 5.Nov.2024, v2: 13.Jul.2025)
- Circular-Convolutional Attention CAT: Circular-Convolutional Attention for Sub-Quadratic Transformers (v1:9.Apr.2025, v2:5.Jan.2026)
- SeerAttention SeerAttention: Learning Intrinsic Sparse Attention in Your LLMs (v1:17.Oct.2024, v4: 17.Feb.2025)
17.1.1. Sparse Attention
A simple but effective way to reduce the computational complexity of attention mechanisms is to make the $QK^{T}$ matrix sparse. This means limiting each position’s attention to a specific subset of other positions, significantly reducing the required computations.
While various methods exist for achieving sparsity, this section focuses on the main approaches.
17.1.1.1. Star-Transformer, LongTransformer, ETC, BigBird
Analysis of many studies using this technique shows that they often combine several basic patterns. The most basic patterns are shown in Fig.17-1:
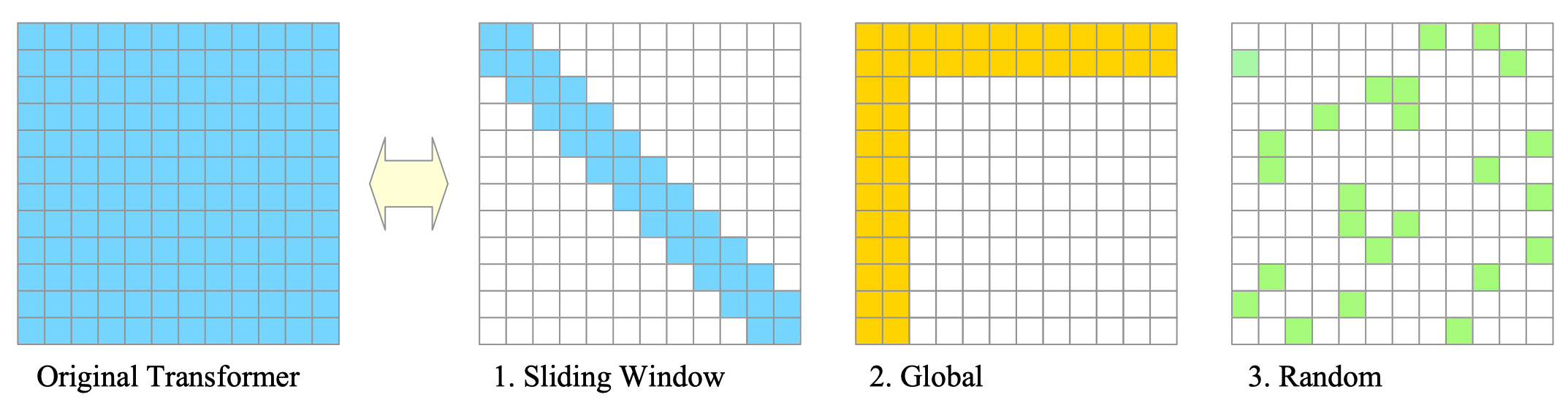
Fig.17-1: (Left) Original Transformer's Attention Pattern. (Right) Basic Sparse Attention Patterns
-
Sliding Window Attention:
Restricts each query to attend only to its neighboring nodes, leveraging the inherent locality of most data. -
Global Attention:
Introduces global nodes as hubs to facilitate efficient information propagation across nodes. -
Random Attention:
Enhances non-local interactions by randomly sampling a few edges for each query, fostering a broader exploration of relationships within the data.
The complexity of these patterns is all $\mathcal{O}(N)$.
The following table and Fig.17-2 joinly show the pattern combinations used by several key variant:
$$ \begin{array} {c|ccc} & \text{Sliding Window} & \text{Global} & \text{Random} \\ \hline \text{Star Transformer} & \checkmark & \checkmark & \\ \text{LongFormer} & \checkmark & \checkmark & \\ \text{ETC} & \checkmark & \checkmark & \\ \text{BigBird} & \checkmark & \checkmark & \checkmark \end{array} $$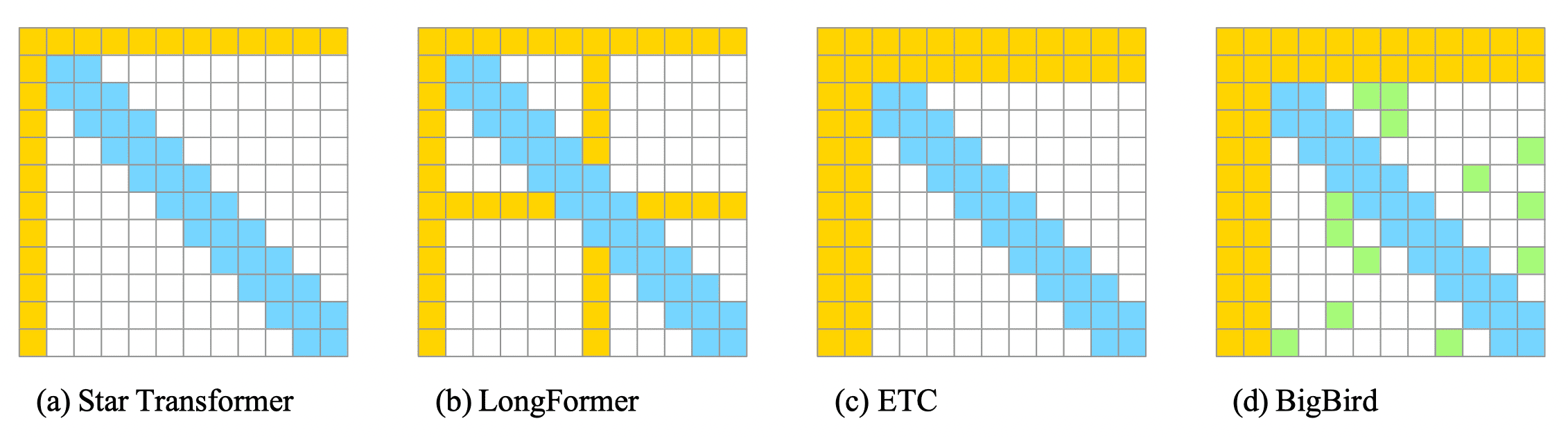
Fig.17-2: Sparse Attention Patterns of Star-Transformer, LongFormer, ETC, and BigBird
- Star-Transformer (v1: 25.Feb.2019, v3: 24.Apr.2022)
- Longformer: The Long-Document Transformer (v1: 10.Apr.2020, v2: 2 Dec 2020)
- ETC: Encoding Long and Structured Inputs in Transformers (v1: 17.Apr.2020, v5: 27.Oct.2020)
- Big Bird: Transformers for Longer Sequences (v1: 28.Jul.2020, v2: 8.Jan.2021)
17.1.1.2. Sparse Transformer
This section explores the Sparse Transformer, an attention mechanism used in the powerful language model GPT-3.
The Sparse Transformer leverages two distinct sparse attention patterns: strided and fixed1.
-
Strided pattern allows the $i$-th output position to attend to the $j$-th input position if one of the two following conditions is satisfied: $(i-s) \lt j \lt (i+s) $ or $ (i-j) \mod s = 0$, where the stride $s$ is chosen to be close to $\sqrt{N}$.
-
Fixed pattern allows the $i$-th output position to attend to the $j$-th input position if one of the two following conditions is satisfied: $ \lfloor \frac{j}{s} \rfloor = \lfloor \frac{i}{s} \rfloor$ or $(s - c) \lt (j \mod s)$, where $c$ is an hyper-parameter.
The complexity of Sparse Transformer is $\mathcal{O}(N \sqrt{N})$, when the stride $s$ is chosen close to $\sqrt{N}$.
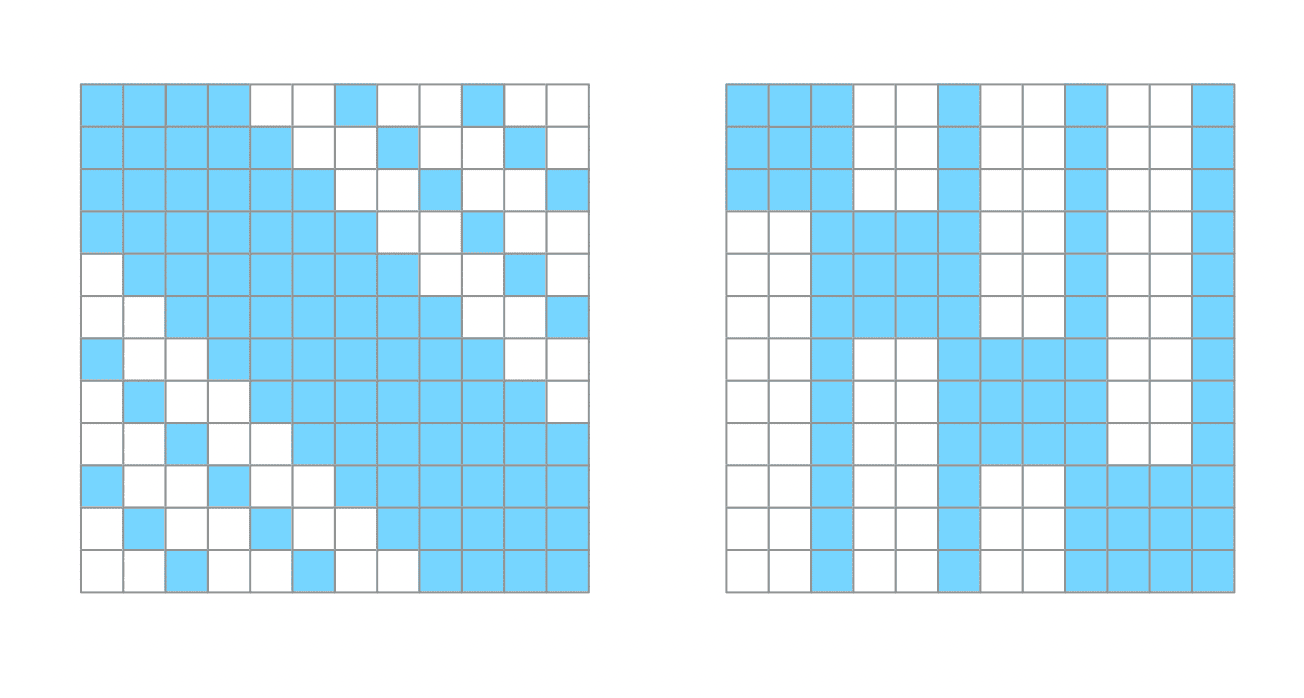
Fig.17-3: Sparse Transformer (Left) Strided Attention with a Stride $s$ of 3. (Right) Fixed Attention with a Stride $s$ of 3 and $c =$ 1.
- Generating Long Sequences with Sparse Transformers (Sparse Transformer) (23.Apr.2019)
- Language Models are Few-Shot Learners (GPT-3) (v1: 28.May.2020, v4: 22.Jul.2020)
17.1.2. Linearized Attention
Linearized attention is a technique that reduces the computational complexity of Transformer models by transforming the softmax function and altering the calculation order.
Imagine replacing the softmax function $\text{softmax}(QK^{T})$ (where $Q, K \in \mathbb{R}^{N \times d_{model}}$) with a new function $Q’K’^{T}$, where $Q’, K’$, and $V \in \mathbb{R}^{N \times d_{model}}$. This allows us to rewrite the attention computation as $Q’(K’^{T} V)$, which simplifies the complexity to $\mathcal{O}(N \cdot d_{model}^2)$, a linear function of the sequence length $N$.
For detailed explanations and specific computation methods, refer to the following papers:
- Efficient Transformers: A Survey in Section 4.2.
- Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention (Linear Transformer) (v1: 29.Jun.2020, v3: 31.Aug.2020)
- Rethinking Attention with Performers (Performer) (v1: 30.Sep.2020, v4: 19.Nov.2022)
- Random Feature Attention (v1: 3.Mar.2021, v2: 19.Mar.2021)
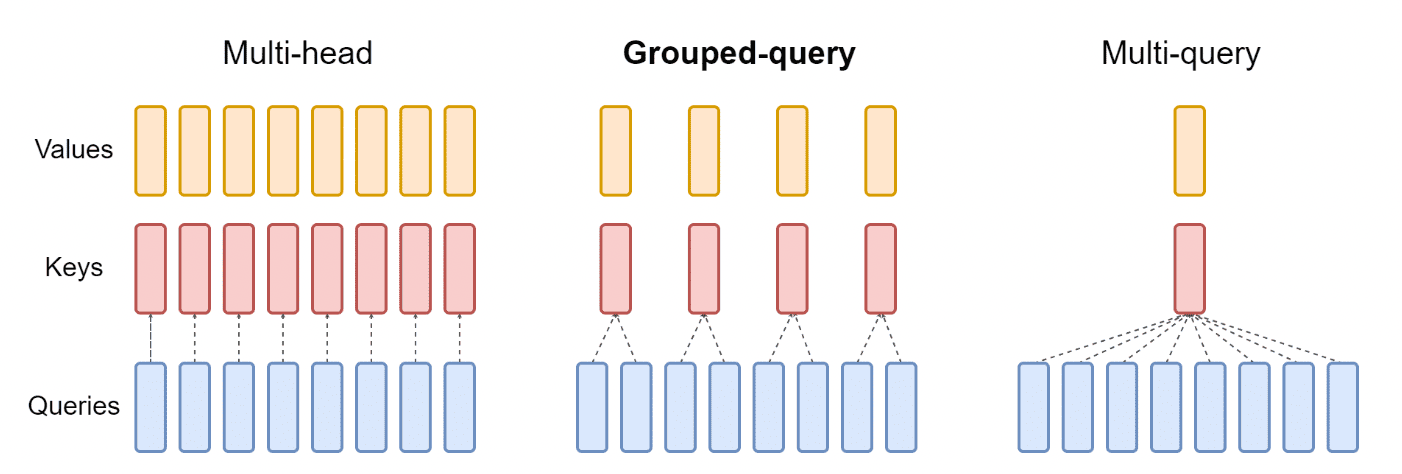
17.1.3. Multi-Query Attention (MQA) and Grouped-Query Attention (GQA)
Introduced in 2019 with the aptly titled paper “Fast Transformer Decoding: One Write-Head is All You Need”, Multi-Query Attention (MQA) aims to improve decoding speed of Transformer models. Its core concept is to utilize the same key and value matrices ($K$ and $V$) for all attention heads within a single layer. This reduces data transfer per computation, leading to faster decoding with minimal quality degradation.
Grouped-Query Attention (GQA), introduced in 2023, expands upon MQA by using multiple, but not all, key-value head groups. This approach addresses the quality degradation observed in MQA while maintaining its efficiency benefits.
Several LLMs have adopted these techniques:
- MQA: Falcon, PaLM
- GQA: LLaMa2, Mistral 7B
- GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints (v1: 22.May.2023, v3: 23.Dec.2023)
- Fast Transformer Decoding: One Write-Head is All You Need (MQA) (6.Nov.2019)
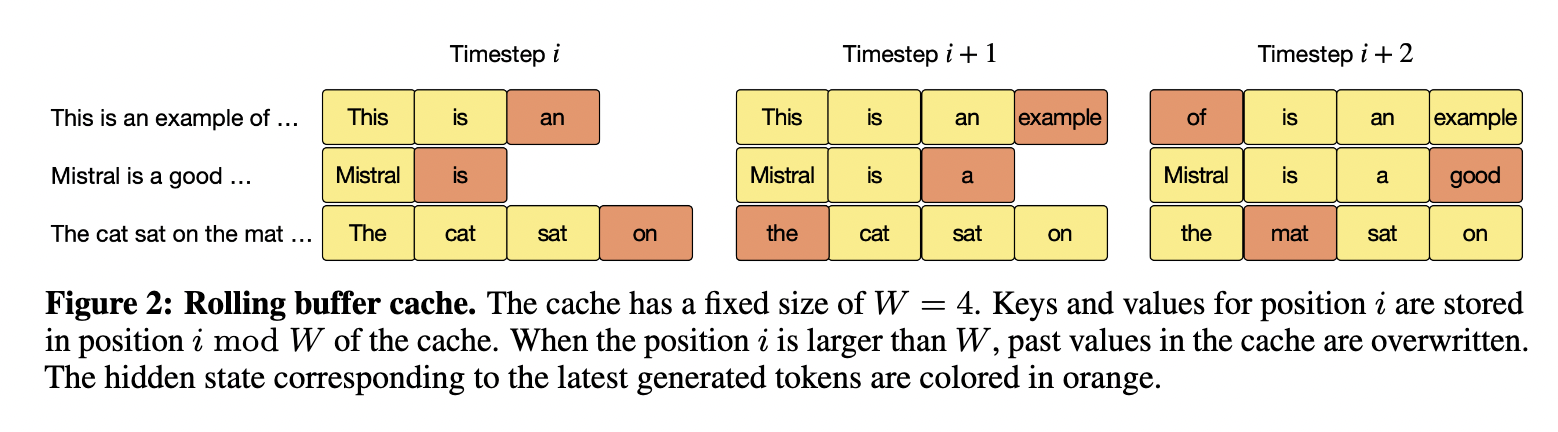
Mistral 7B employs several innovative techniques to optimize performance. These includes:
- Rolling Buffer Cache: Enables efficient access to recently processed data.
- Pre-fill and Chunking: Facilitates smoother data processing for large prompts (input or output sentences).
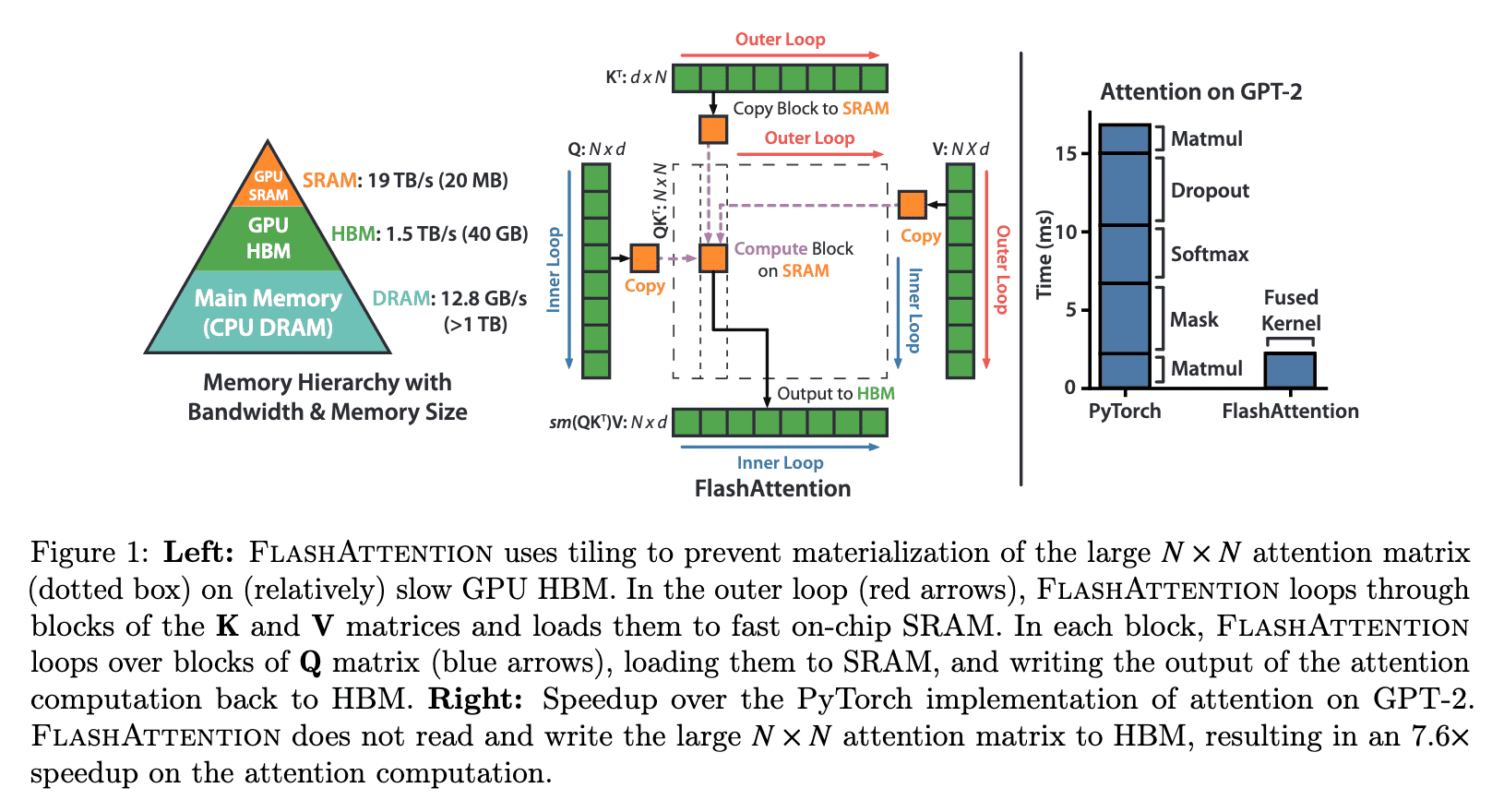
17.1.4. FlashAttention
Unlike methods that focus on simplifying calculations, FlashAttention takes a different approach. It leverages the capabilities of GPUs to optimize attention computation efficiently without introducing approximations. This results in faster and more accurate attention processing compared to traditional methods.
The following figure, taken from the research paper, illustrates the key idea behind FlashAttention:
With minimal code modifications, existing Transformer models can integrate FlashAttention for speedups.
This method is readily available through popular platforms like Hugging Face and AWS.
Furthermore, major LLMs like MPT and Falcon have already adopted FlashAttention.
- FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness (v1: 27.May.2022, v2: 23.Jun.2022)
- FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning (v1: 17.Jul.2023)
17.1.5. Quantization
Quantization is a fundamental technique in computer science for reducing computational resources. It achieves this by lowering the precision of data representations, such as memory footprint and the number of required operations.
This technique is also applied in the field of LLMs. For example, many LLMs utilize lower precision formats, such as 8-bit or 4-bit integers, for their computations, instead of the 32-bit floating-point numbers.
- A Survey of Quantization Methods for Efficient Neural Network Inference (v1:25.Mar.2021, v3:21.Jun.2021)
- A Survey on Model Compression for Large Language Models (v1:15.Aug.2023, v4:30.Jul.2024)
-
display-sparse-attentions.py displays the the strided and fixed attentions for any parameters: N, s, c. ↩︎