8.5. Back Propagation Through Time in Many-to-Many type
The formulation of the Many-to-Many LSTM with dense layers is defined as follows:
$$ \begin{cases} f^{(t)} = \sigma(W_{f} x^{(t)} + U_{f} h^{(t-1)} + b_{f}) \\ i^{(t)} = \sigma(W_{i} x^{(t)} + U_{i} h^{(t-1)} + b_{i}) \\ \tilde{C}^{(t)} = \tanh(W_{c} x^{(t)} + U_{c} h^{(t-1)} + b_{c}) \\ C^{(t)} = f_{(t)} \odot C^{(t-1)} + i^{(t)} \odot \tilde{C}^{(t)} \\ o^{(t)} = \sigma(W_{o} x^{(t)} + U_{o} h^{(t-1)} + b_{o}) \\ h^{(t)} = o^{(t)} \odot \tanh(C^{(t)}) \\ \hat{y}^{(t)} = V h^{(t)} + c \\ y^{(t)} = g(\hat{y}^{(t)}) \end{cases} \tag{8.24} $$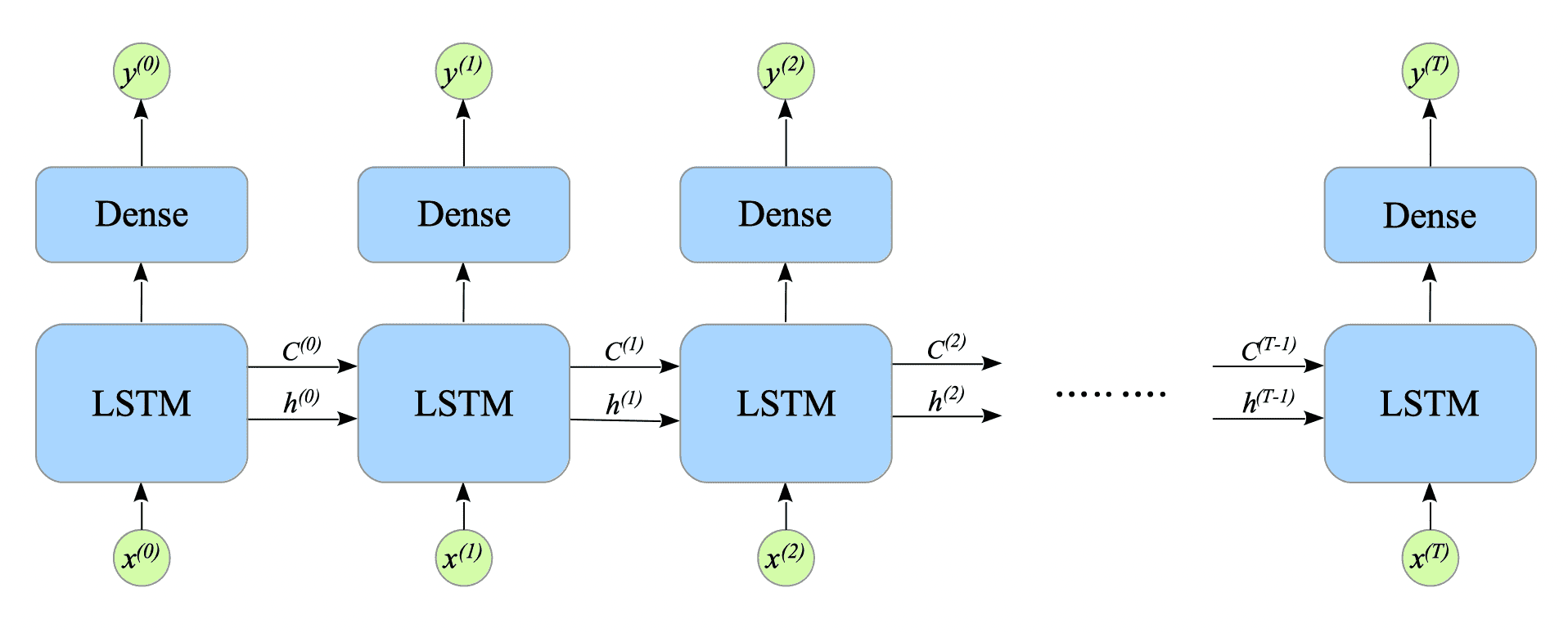
Fig.8-8: Many-to-Many LSTM
8.5.1. Computing the gradients for Back Propagation Through Time
We use the mean squared error (MSE) as the loss function $L$, defined as follows:
$$ L = \sum_{t=0}^{T} \frac{1}{2} (y^{(t)} - Y^{(t)})^{2} \tag{8.25} $$For convenience, we define $L^{(t)}$, the loss value at time step $t$:
$$ L^{(t)} \stackrel{\mathrm{def}}{=} \frac{1}{2} (y^{(t)} - Y^{(t)})^{2} \tag{8.26} $$Thus, the loss function $L$ can be represented as follows:
$$ L = \sum_{t=0}^{T} L^{(t)} \tag{8.27} $$To simplify the following discussion, we define the following expression:
$$ \text{grad}_{dense}^{(t)} \stackrel{\mathrm{def}}{=} \frac{\partial L^{(t)}}{\partial h^{(t)}} \tag{8.28} $$$ \text{grad}_{dense}^{(t)}$ is the gradient propagated from the dense layer at time step $t$.
Using these expressions, we can build the backward computational graph. Fig.8-9 illustrates the relationship between $h^{(T)}$ and $h^{(T-1)}$.

Fig.8-9: Relationship Between $h^{(T)}$, $h^{(T-1)}$, and Dense Layer Outputs
For an explanation of computational graphs, see Appendix.
Similar to the case with SimpleRNN, we can derive $dh^{(t)}$ for a many-to-many LSTM from expression $(8.8)$ as follows:
$$ dh^{(t)} = \begin{cases} \text{grad}_{dense}^{(t)} & t = T \\ \\ \begin{align} & \text{grad}_{dense}^{(t)} + dh^{(t+1)} \tanh(C^{(t+1)}) \sigma'(W_{o} x^{(t+1)} + U_{o} h^{(t)} + b_{o}) \ {}^t U_{o} \\ & \quad + dh^{(t+1)} o^{(t+1)} \odot \tanh'(C^{(t+1)}) \tilde{C}^{(t+1)} \sigma'(W_{i} x^{(t+1)} + U_{i} h^{(t)} + b_{i}) \ {}^t U_{i} \\ & \quad + dh^{(t+1)} o^{(t+1)} \odot \tanh'(C^{(t+1)}) i^{(t+1)} \tanh'(W_{c} x^{(t+1)} + U_{c} h^{(t)} + b_{c}) \ {}^t U_{c} \\ & \quad + dh^{(t+1)} o^{(t+1)} \odot \tanh'(C^{(t+1)}) C^{(t)} \sigma'(W_{f} x^{(t+1)} + U_{f} h^{(t)} + b_{f}) \ {}^t U_{f} \end{align} & 0 \le t \lt T \end{cases} \tag{8.29} $$To avoid confusion, we express the transpose of a vector or matrix $ A $ as $ \ {}^tA$, instead of $A^{T}$, in this section.
Using $dh^{(t)}$ defined in $(8.29)$, we can also calculate $dC^{(t)}$ defined in $(8.11)$.
Finally, we can obtain the gradients defined in expressions $(8.12)-(8.23)$, using the $dh^{(t)}$ and $dC^{(t)}$ defined here.