6. Dataset and Task

In this part, we tackle sine wave prediction, a common task in regression problems.

6.1. Dataset

DataSet.py module provides two functions: create_wave() and dataset().

6.1.1. create_wave() function

The create_wave() function generates a sequence of data $S =$ {$s_{0},s_{1},\ldots,s_{N-1}$} representing a sine wave with amplitude 1 and 2 cycles, specified by the number $N$. The default value of $N$ is $100$.

def create_wave(N=100, noise=0.05):
    _x_range = np.linspace(0, 2 * 2 * np.pi, N)
    return np.sin(_x_range) + noise * np.random.randn(len(_x_range))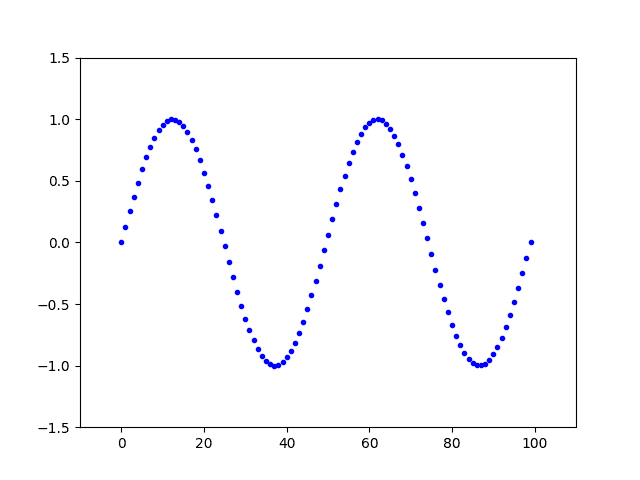

6.1.2. dataset() function

The dataset() function creates a given data sequence $S$ and the value $n$ into a suitable dataset for training a regression model. It operates as follows:

1. Creating the first training example:
   1. Extract the first n elements of $S$, from $s_{0}$ to $s_{n-1}$, as the input sequence $x_{0}$.
   2. Set the next element $s_{n}$ as the corresponding output label $y_{0}$.
   3. This creates the first training example, $(x_{0}, y_{0})$, aiming to predict $s_{n}$ based on the preceding $n$ points.
2. Generating more training examples:
   • Repeat for $j = 1$ to $N-n-1$:
     • Extract a new input sequence $x_{j}$ from $s_{j}$ to $s_{j+n-1}$.
     • Set the corresponding output label $y_{j}$.

This dataset{$(x_{0},y_{0}),(x_{1},y_{1}),\ldots,(x_{N-n-1},y_{N-n-1}) $} can then be used to train a regression model to predict the next data point in the sequence.

def dataset(S, n=25):
    n_sample = len(S) - n

    x = np.zeros((n_sample, n, 1, 1))
    y = np.zeros((n_sample, 1, 1))

    for i in range(n_sample):
        x[i, :, 0, 0] = S[i : i + n]
        y[i, 0] = S[i + n]

    return x, y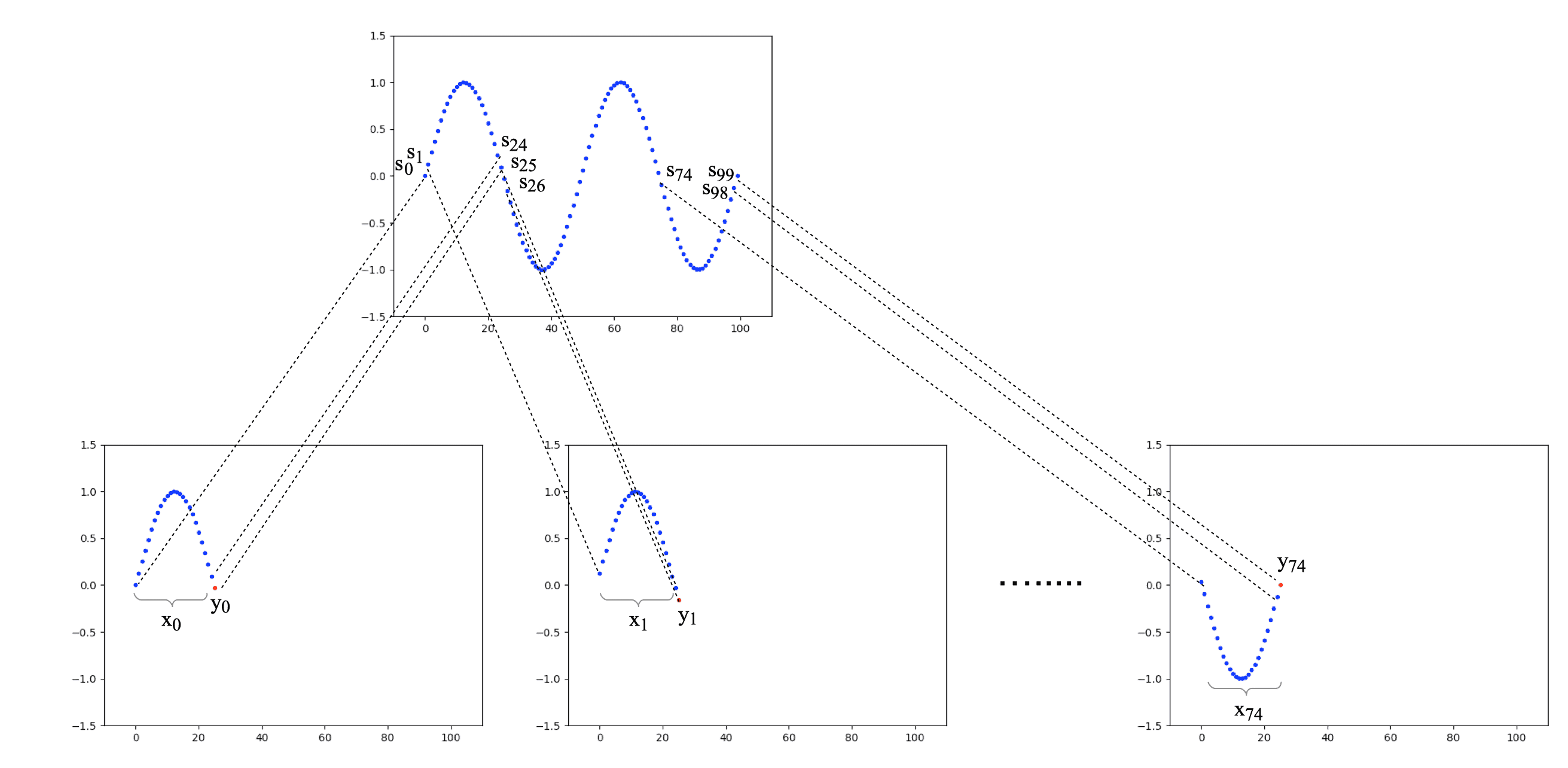

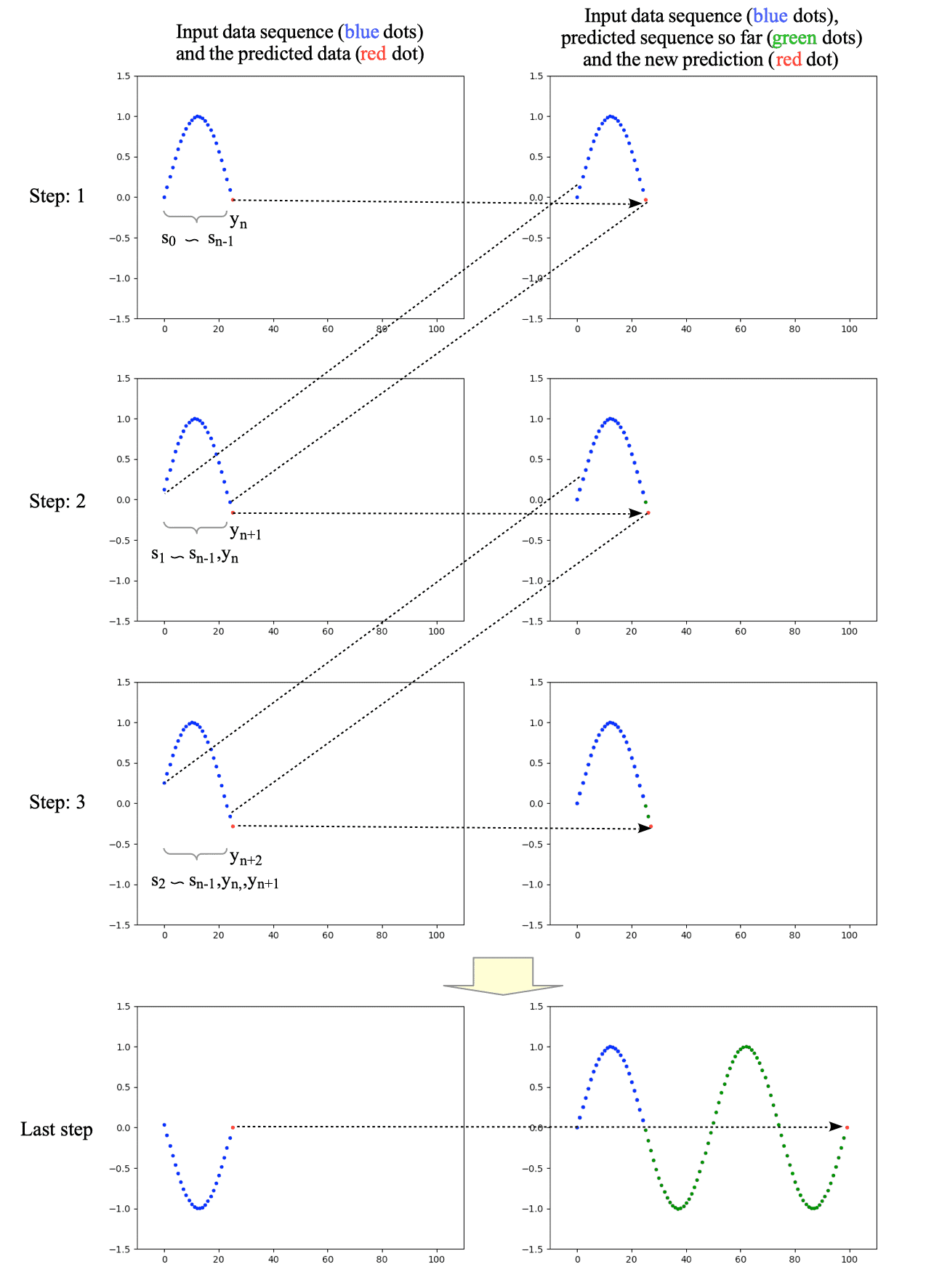
6.2. Prediction Task

To make predictions, we use a method called $k$-step-ahead prediction:

1. Predict $y_{n}$ using $s_0$ to $s_{n-1}$ in the data sequence $S$ (i.e., the data sequence $x_{0}$).
2. Predict $y_{n+1}$ using the data sequence $s_{1}$ to $s_{n-1}$ and the previous predicted value $y_{n}$.
3. Similarly, for $j = n+2$ to $N-n-1$, we take the predicted value $y_{j}$ and continue prediction.