9.3. Implementation
Complete Python code is available at: GRU_from_scrtch.py.
The GRU class is shown below:
class GRU:
def __init__(self, input_units, hidden_units, return_sequences=False):
self.return_sequences = return_sequences
self.input_units = input_units
self.hidden_units = hidden_units
"""
Initialize random weights and bias using Glorot
and Orthogonal Weight Initializations.
Glorat Weight Initialization: Glorot & Bengio, AISTATS 2010
http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
Orthogonal Weight Initialization: Saxe et al.,
https://arxiv.org/pdf/1312.6120.pdf
"""
self.Wz = np.random.randn(hidden_units, input_units) * np.sqrt(2.0 / (hidden_units + input_units))
self.Wr = np.random.randn(hidden_units, input_units) * np.sqrt(2.0 / (hidden_units + input_units))
self.W = np.random.randn(hidden_units, input_units) * np.sqrt(2.0 / (hidden_units + input_units))
self.Uz = np.random.randn(hidden_units, hidden_units) * np.sqrt(2.0 / (2 * hidden_units))
self.Uz, _, _ = np.linalg.svd(self.Uz) # Orthogonal Weight Initialization
self.Ur = np.random.randn(hidden_units, hidden_units) * np.sqrt(2.0 / (2 * hidden_units))
self.Ur, _, _ = np.linalg.svd(self.Ur) # Orthogonal Weight Initialization
self.U = np.random.randn(hidden_units, hidden_units) * np.sqrt(2.0 / (2 * hidden_units))
self.U, _, _ = np.linalg.svd(self.U) # Orthogonal Weight Initialization
self.bz = np.random.randn(hidden_units, 1) * np.sqrt(2.0 / (1 + hidden_units))
self.br = np.random.randn(hidden_units, 1) * np.sqrt(2.0 / (1 + hidden_units))
self.b = np.random.randn(hidden_units, 1) * np.sqrt(2.0 / (1 + hidden_units))
def get_grads(self):
return [self.dWz, self.dWr, self.dW,
self.dUz, self.dUr, self.dU,
self.dbz, self.dbr, self.db]
def get_params(self):
return [self.Wz, self.Wr, self.W,
self.Uz, self.Ur, self.U,
self.bz, self.br, self.b]
def forward_prop(self, x, n_sequence):
self.x = x
self.n_sequence = n_sequence
self.z = np.zeros([self.n_sequence, self.hidden_units, 1])
self.z_p = np.zeros([self.n_sequence, self.hidden_units, 1])
self.r = np.zeros([self.n_sequence, self.hidden_units, 1])
self.r_p = np.zeros([self.n_sequence, self.hidden_units, 1])
self.h_h = np.zeros([self.n_sequence, self.hidden_units, 1])
self.h_h_p = np.zeros([self.n_sequence, self.hidden_units, 1])
self.h = np.zeros([self.n_sequence, self.hidden_units, 1])
for t in range(self.n_sequence):
if t == 0:
self.z_p[t] = np.dot(self.Wz, self.x[t]) + self.bz
self.z[t] = sigmoid(self.z_p[t])
self.r_p[t] = np.dot(self.Wr, self.x[t]) + self.br
self.r[t] = sigmoid(self.r_p[t])
self.h_h_p[t] = np.dot(self.W, self.x[t]) + self.b
self.h_h[t] = tanh(self.h_h_p[t])
self.h[t] = self.z[t] * self.h_h[t]
else:
self.z_p[t] = (np.dot(self.Wz, self.x[t]) + np.dot(self.Uz, self.h[t - 1]) + self.bz)
self.z[t] = sigmoid(self.z_p[t])
self.r_p[t] = (np.dot(self.Wr, self.x[t]) + np.dot(self.Ur, self.h[t - 1]) + self.br)
self.r[t] = sigmoid(self.r_p[t])
self.h_h_p[t] = (np.dot(self.W, self.x[t]) + np.dot(self.U, self.r[t] * self.h[t - 1]) + self.b)
self.h_h[t] = tanh(self.h_h_p[t])
self.h[t] = (1 - self.z[t]) * self.h[t - 1] + self.z[t] * self.h_h[t]
if self.return_sequences == False:
return self.h[-1]
else:
return self.h
def back_prop(self, grads):
dh = np.zeros([self.n_sequence, self.hidden_units, 1])
dx = np.zeros([self.n_sequence, self.input_units, 1])
# Compute dh from time step T backward through 0.
for t in reversed(range(self.n_sequence)):
if t == self.n_sequence - 1:
if self.return_sequences == True:
dh[t] = grads[t]
else:
dh[t] = grads
else:
d1 = np.dot(self.Uz.T, dh[t + 1] * (self.h_h[t + 1] - self.h[t]) * deriv_sigmoid(self.z_p[t + 1]))
d2 = np.dot(self.r[t + 1] * self.U.T, dh[t + 1] * self.z[t + 1] * deriv_tanh(self.h_h_p[t + 1]))
d3 = np.dot(self.Ur.T, np.dot(self.h[t] * self.U.T, dh[t + 1] * self.z[t + 1] * deriv_tanh(self.h_h_p[t + 1])) * deriv_sigmoid(self.r_p[t + 1]))
d4 = dh[t + 1] * (1 - self.z[t + 1])
dh[t] = d1 + d2 + d3 + d4
if self.return_sequences == True:
dh[t] += grads[t]
# Compute the gradients of the weights and biases from time step 0 through T.
for t in range(self.n_sequence):
if t > 0:
_dbz = (dh[t] * deriv_sigmoid(self.z_p[t]) * (self.h_h[t] - self.h[t - 1]))
else:
_dbz = dh[t] * deriv_sigmoid(self.z_p[t]) * self.h_h[t]
self.dbz += _dbz
self.dWz += np.dot(_dbz, self.x[t].T)
if t > 0:
self.dUz += np.dot(_dbz, self.h[t - 1].T)
if t > 0:
_dbr = np.dot(self.h[t - 1] * self.U.T, dh[t] * self.z[t] * deriv_tanh(self.h_h_p[t])) * deriv_sigmoid(self.r_p[t])
self.dbr += _dbr
self.dWr += np.dot(_dbr, self.x[t].T)
self.dUr += np.dot(_dbr, self.h[t - 1].T)
_db = dh[t] * self.z[t] * deriv_tanh(self.h_h_p[t])
self.db += _db
self.dW += np.dot(_db, self.x[t].T)
if t > 0:
self.dU += np.dot(_db, (self.r[t] * self.h[t - 1]).T)
dx[t] = np.dot(self.Wz.T, _dbz) + np.dot(self.W.T, _db)
if t > 0:
dx[t] += np.dot(self.Wr.T, _dbr)
return dxThe back_prop() method consists of two key steps:
-
Computing hidden state gradients: This loop iterates backward through time steps, starting from the final step $T$ and ending at $0$, to calculate the gradient of the hidden state at each step, denoted as $dh[t]$.
-
Calculating parameter gradients: Based on the computed hidden state gradients, this step calculates the gradients of the model’s parameters, with respect to the hidden state gradients.
[1] Create dataset.
# ============================
# Create Dataset
# ============================
n_sequence = 25
n_data = 100
n_sample = n_data - n_sequence # number of samples
sin_data = ds.create_wave(n_data, 0.05)
X, Y = ds.dataset(sin_data, n_sequence)[2] Create model.
We construct a simple RNN layer followed by a dense layer. The dense layer employs a linear activation function.
# ============================
# Create Model
# ============================
input_units = 1
hidden_units = 32
output_units = 1
gru = GRU(input_units, hidden_units)
dense = Layers.Dense(hidden_units, output_units, linear, deriv_linear)[3] Training.
This model’s training function is identical to the neural network training functions introduced so far.
# ============================
# Training
# ============================
def train(gru, dense, X, Y, optimizer):
# Forward Propagation
last_h = gru.forward_prop(X, n_sequence)
y = dense.forward_prop(last_h)
# Back Propagation Through Time
loss = np.sum((y - Y) ** 2 / 2)
dL = y - Y
grads = dense.back_prop(dL)
_ = gru.back_prop(grads)
update_weights([dense, gru], optimizer=optimizer)
return loss
n_epochs = 200
lr = 0.0001
beta1 = 0.99
beta2 = 0.9999
optimizer = Optimizer.Adam(lr=lr, beta1=beta1, beta2=beta2)
for epoch in range(1, n_epochs + 1):
loss = 0.0
for j in range(n_sample):
loss += train(gru, dense, X[j], Y[j], optimizer)[4] Prediction.
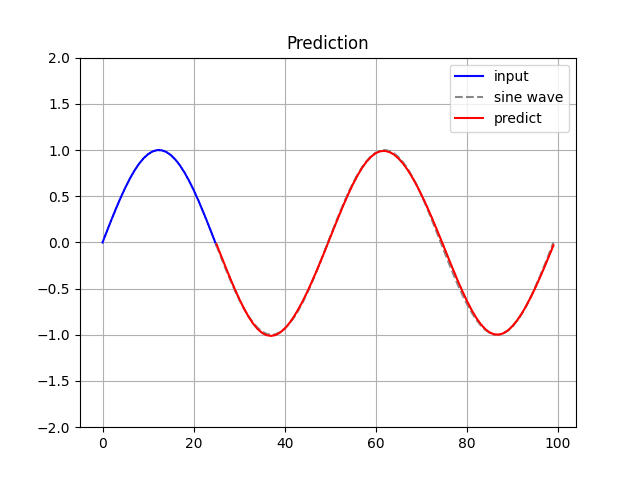
Run the following command to generate and display the predicted sine wave:
$ python GRU_from_scratch.py
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
gru (GRU) (None, 25, 32) 3264
dense (Dense) (None, 25, 1) 33
=================================================================
Total params: 3297
epoch: 10/200 Loss = 0.413963
epoch: 20/200 Loss = 0.246206
epoch: 30/200 Loss = 0.212136
epoch: 40/200 Loss = 0.193578
epoch: 50/200 Loss = 0.182354
epoch: 60/200 Loss = 0.174332
epoch: 70/200 Loss = 0.167752
epoch: 80/200 Loss = 0.161927
epoch: 90/200 Loss = 0.156588
epoch: 100/200 Loss = 0.151625
epoch: 110/200 Loss = 0.146991
epoch: 120/200 Loss = 0.142664
epoch: 130/200 Loss = 0.138625
epoch: 140/200 Loss = 0.134861
epoch: 150/200 Loss = 0.131355
epoch: 160/200 Loss = 0.128090
epoch: 170/200 Loss = 0.125049
epoch: 180/200 Loss = 0.122215
epoch: 190/200 Loss = 0.119574
epoch: 200/200 Loss = 0.117109