7.1. Formulation of Simple RNN
The formulation of the simple RNN is defined as follows:
$$ \begin{cases} \hat{h}^{(t)} = W x^{(t)} + U h^{(t-1)} + b \\ h^{(t)} = f(\hat{h}^{(t)}) \end{cases} \tag{7.1} $$Given that the number of input nodes and hidden nodes are $ m $ and $ h $, respectively, then:
- $ x^{(t)} \in \mathbb{R}^{m} $ is the input at time $t$.
- $ h^{(t)} \in \mathbb{R}^{h} $ is the hidden state at time $t$.
- $ W \in \mathbb{R}^{h \times m}$ and $U \in \mathbb{R}^{h \times h}$ are the weights matrices.
- $ b \in \mathbb{R}^{m}$ is the bias term.
- $ f(\cdot) $ is the activation function.
Fig.7-3 illustrates the simple RNN defined above:
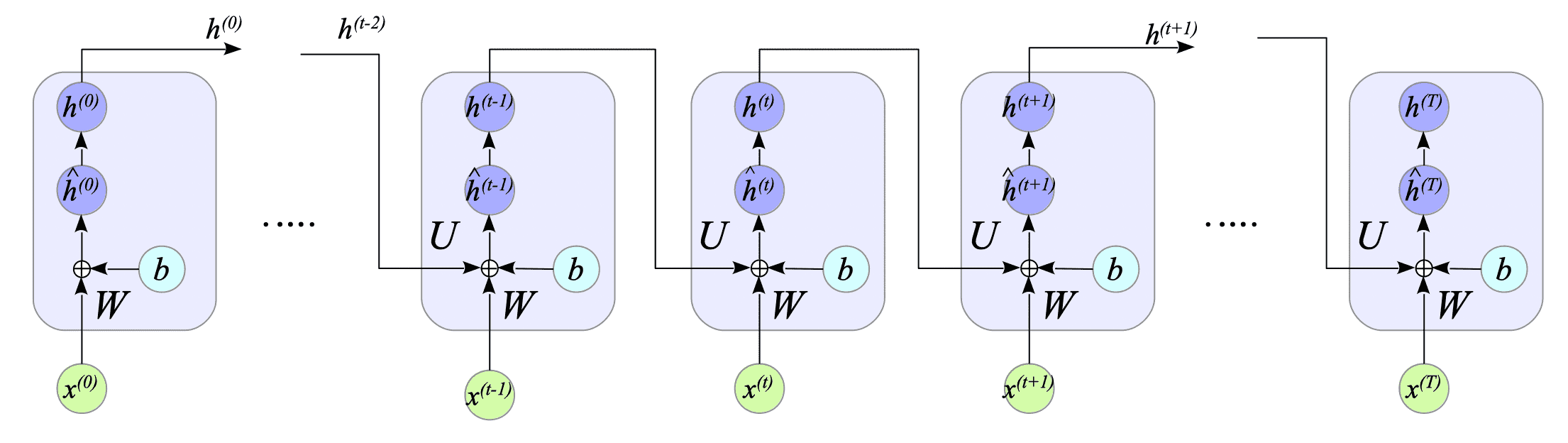
Fig.7-3: Simple RNN Architecture
Since the SimpleRNN lacks an output layer, we add a dense layer (also known as a fully connected layer) to extract the final hidden state. This makes it a many-to-one RNN. See Fig.7-4.
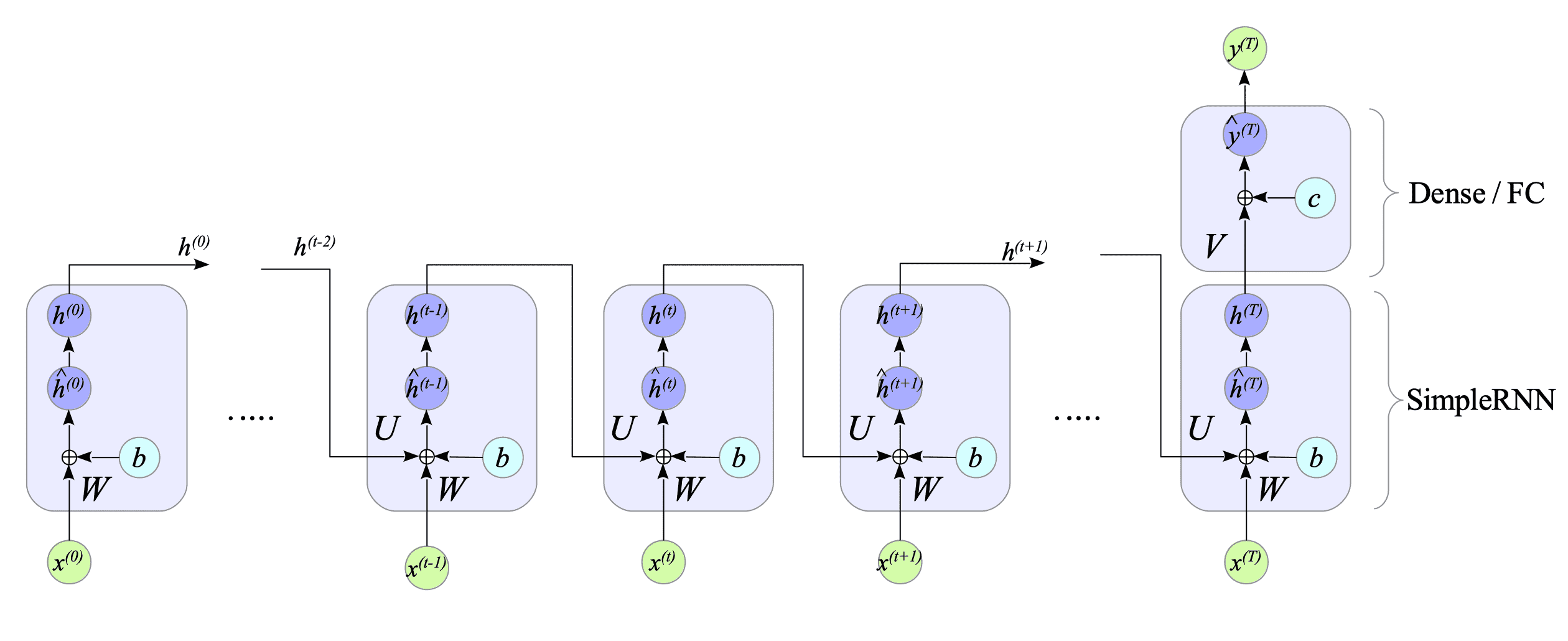
Fig.7-4: Many-to-One Simple-RNN
Given that the number of output nodes is $ n $. Then, the dense layer is defined as follows:
$$ \begin{cases} \hat{y}^{(T)} = V h^{(T)} + c \\ y^{(T)} = g(\hat{y}^{(T)}) \end{cases} \tag{7.2} $$where:
- $ V \in \mathbb{R}^{n \times h} $ is the weight matrix.
- $ c \in \mathbb{R}^{n} $ is the bias term.
- $ y^{(T)} \in \mathbb{R}^{n} $ is the output vector.
- $ g(\cdot) $ is the activation function.